Suvarna Garge (Editor)

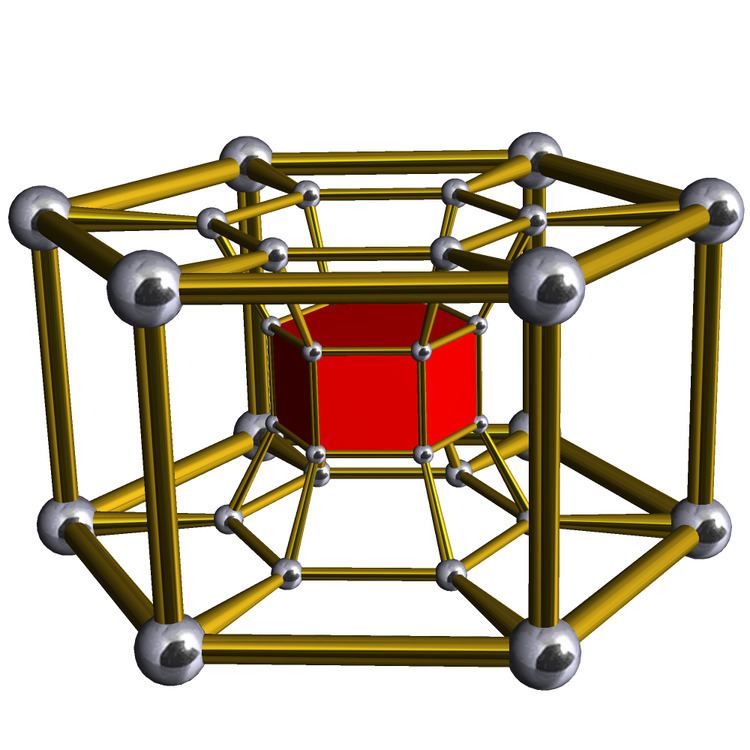
6 6 duoprism

Updated on
Edit
Like
Comment
Share on FacebookTweet on TwitterShare on LinkedInShare on Reddit
6-6 duoprism

In geometry of 4 dimensions, a 6-6 duoprism is a polygonal duoprism, a 4-polytope resulting from the Cartesian product of two octagons.

Contents

It has 36 vertices, 72 edges, 48 faces (36 squares, and 12 hexagons), in 12 hexagonal prism cells. It has Coxeter diagram , and symmetry [[6,2,6]], order 288.

Images


Net

Seen in a skew 2D orthogonal projection, it contains the projected rhombi of the rhombic tiling.

The regular complex polytope 6{4}2, , in C 2 has a real representation as a 6-6 duoprism in 4-dimensional space. 6{4}2 has 36 vertices, and 12 6-edges. Its symmetry is 6[4]2, order 72. It also has a lower symmetry construction, , or 6{}×6{}, with symmetry 6[2]6, order 36. This is the symmetry if the red and blue 6-edges are considered distinct.

6-6 duopyramid

The dual of a 6-6 duoprism is called a 6-6 duopyramid. It has 36 tetragonal disphenoid cells, 72 triangular faces, 48 edges, and 12 vertices.

It can be seen in orthogonal projection:

The regular complex polygon 2{4}6 or has 12 vertices in C 2 with a real represention in R 4 matching the same vertex arrangement of the 6-6 duopyramid. It has 36 2-edges corresponding to the connecting edges of the 6-6 duopyramid, while the 12 edges connecting the two hexagons are not included.

The vertices and edges makes a complete bipartite graph with each vertex from one pentagon is connected to every vertex on the other.

References

6-6 duoprism Wikipedia
(Text) CC BY-SA


Similar Topics