Vertices Infinite Rotation group [5,4], (542) | Edges Infinite Symmetry group [5,4], (*542) | |
 | ||
Type Dual semiregular hyperbolic tiling | ||
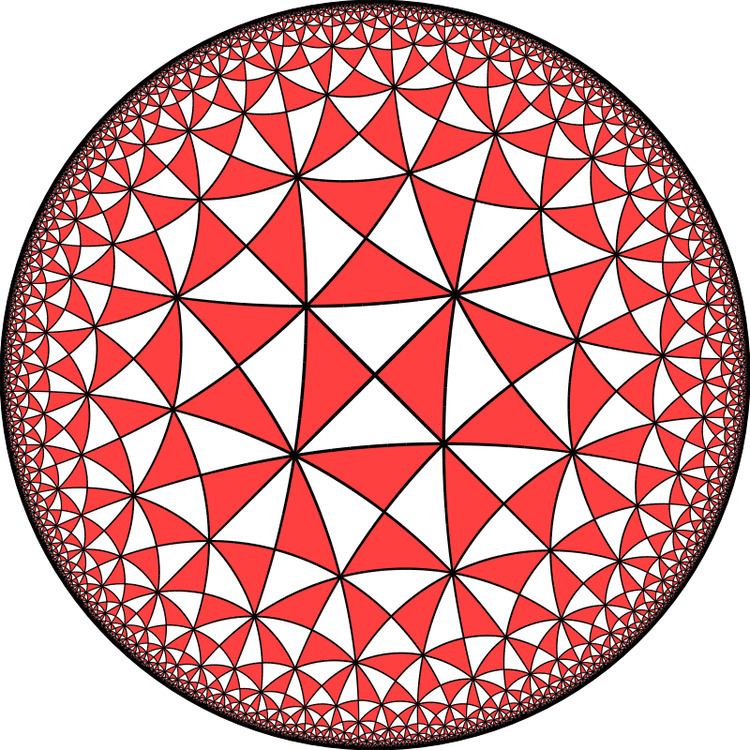
In geometry, the 4-5 kisrhombille or order-4 bisected pentagonal tiling is a semiregular dual tiling of the hyperbolic plane. It is constructed by congruent right triangles with 4, 8, and 10 triangles meeting at each vertex.
The name 4-5 kisrhombille is by Conway, seeing it as a 4-5 rhombic tiling, divided by a kis operator, adding a center point to each rhombus, and dividing into four triangles.
The image shows a Poincaré disk model projection of the hyperbolic plane.
It is labeled V4.8.10 because each right triangle face has three types of vertices: one with 4 triangles, one with 8 triangles, and one with 10 triangles.
Dual tiling
It is the dual tessellation of the truncated tetrapentagonal tiling which has one square and one octagon and one decagon at each vertex.
