 | ||
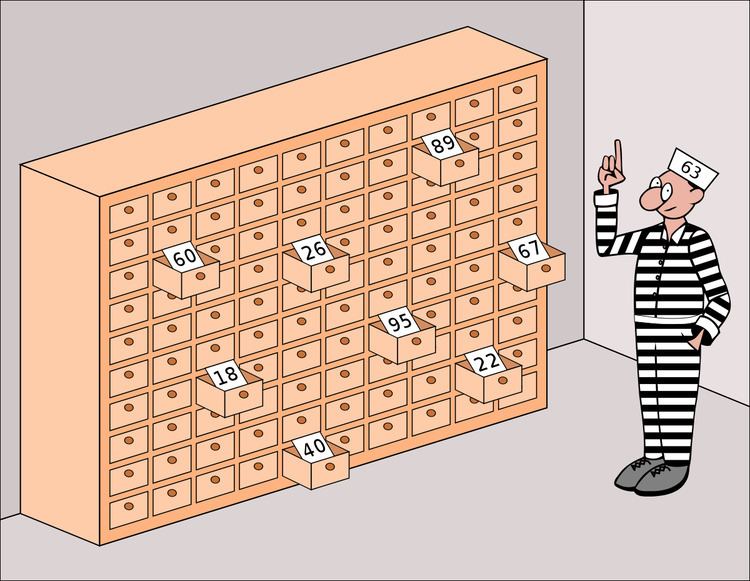
The 100 prisoners problem is a mathematical problem in probability theory and combinatorics. In this problem, 100 numbered prisoners, to survive, must find their own numbers in one of 100 drawers. The rules state that each prisoner may open only 50 drawers, and cannot communicate with other prisoners. At first glance the situation appears hopeless—but a clever strategy offers the prisoners a realistic chance of survival. Danish computer scientist Peter Bro Miltersen first proposed the problem in 2003.
Contents
Problem
The 100 prisoners problem has different renditions in the literature. The following version is by Philippe Flajolet and Robert Sedgewick:
The director of a prison offers 100 death row prisoners, who are numbered from 1 to 100, a last chance. A room contains a cupboard with 100 drawers. The director randomly puts one prisoner's number in each closed drawer. The prisoners enter the room, one after another. Each prisoner may open and look into 50 drawers in any order. The drawers are closed again afterwards. If, during this search, every prisoner finds his number in one of the drawers, all prisoners are pardoned. If just one prisoner does not find his number, all prisoners die. Before the first prisoner enters the room, the prisoners may discuss strategy—but may not communicate once the first prisoner enters to look in the drawers. What is the prisoners' best strategy?If every prisoner selects 50 drawers at random, the probability that a single prisoner finds his number is 50%. Therefore, the probability that all prisoners find their numbers is the product of the single probabilities, which is (1/2)100 ≈ 6969800000000000000♠0.0000000000000000000000000000008, a vanishingly small number. The situation appears hopeless.
Strategy
Surprisingly, there is a strategy that provides a survival probability of more than 30%. The key to success is that the prisoners do not have to decide beforehand which drawers to open. Each prisoner can use the information gained from the contents of previously opened drawers to help decide which drawer to open next. Another important observation is that this way the success of one prisoner is not independent of the success of the other prisoners.
To describe the strategy, not only the prisoners, but also the drawers are numbered from 1 to 100, for example row by row starting with the top left drawer. The strategy is now as follows:
- Each prisoner first opens the drawer with his own number.
- If this drawer contains his number he is done and was successful.
- Otherwise, the drawer contains the number of another prisoner and he next opens the drawer with this number.
- The prisoner repeats steps 2 and 3 until he finds his own number or has opened 50 drawers.
This approach ensures that every time a prisoner opens a drawer, he either finds his own number or the number of another prisoner he has not yet encountered.
Examples
The reason this is a promising strategy is illustrated with the following example using eight prisoners and drawers, whereby each prisoner may open four drawers. The prison director has distributed the prisoners' numbers into the drawers in the following fashion
The prisoners now act as follows:
In this case, all prisoners find their numbers. This is, however, not always the case. In the following example the prison director has distributed the numbers like this:
In this case, prisoner 1 opens drawers 1, 3, 7, and 4, at which point he has to stop unsuccessfully. Except for prisoner 6, who directly finds his number, all other prisoners are also unsuccessful.
Permutation representation
The prison director's assignment of prisoner numbers to drawers can mathematically be described as a permutation of the numbers 1 to 100. Such a permutation is a one-to-one mapping of the set of natural numbers from 1 to 100 to itself. A sequence of numbers which after repeated application of the permutation returns to the first number is called a cycle of the permutation. Every permutation can be decomposed into disjoint cycles, that is, cycles which have no common elements. The permutation of the first example above can be written in cycle notation as
and thus consists of two cycles of length 3 and one cycle of length 2. The permutation of the second example is accordingly
and consists of a cycle of length 7 and a cycle of length 1. The cycle notation is not unique since a cycle of length
Probability of success
In the initial problem, the 100 prisoners are successful if the longest cycle of the permutation has a length of at most 50. Their survival probability is therefore equal to the probability that a random permutation of the numbers 1 to 100 contains no cycle of length greater than 50. This probability is determined in the following.
A permutation of the numbers 1 to 100 can contain at most one cycle of length
The probability, that a (uniformly distributed) random permutation contains no cycle of length greater than 50 is with the formula for single events and the formula for complementary events thus given by
where
Asymptotics
If
With the Euler–Mascheroni constant
holds, which results in an asymptotic survival probability of
Since the sequence of probabilities is monotonically decreasing, the prisoners survive with the cycle-following strategy in more than 30% of cases independently of the number of prisoners.
Optimality
In 2006, Eugene Curtin and Max Warshauer gave a proof for the optimality of the cycle-following strategy. The proof is based on an equivalence to a related problem in which all prisoners are allowed to be present in the room and observe the opening of the drawers. Mathematically, this equivalence is based on Foata's transition lemma, a one-to-one correspondence of the (canonical) cycle notation and the one-line notation of permutations. In the second problem, the survival probability is independent of the chosen strategy and equal to the survival probability in the original problem with the cycle-following strategy. Since an arbitrary strategy for the original problem can also be applied to the second problem, but cannot attain a higher survival probability there, the cycle-following strategy has to be optimal.
History
The 100 prisoners problem was first considered in 2003 by Danish computer scientist Peter Bro Miltersen who published it with Anna Gál in the proceedings of the 30. International Colloquium on Automata, Languages and Programming (ICALP). In their version, player A (the prison director) randomly colors strips of paper with the names of the players of team B (the prisoners) in red or blue and puts each strip into a different box. Every player of team B must guess his color correctly after opening half of the boxes for their team to win. Initially, Milterson assumed that the winning probability quickly tends to zero with increasing number of players. Sven Skyum, a colleague of Miltersen at Aarhus University, however brought his attention to the cycle-following strategy. To find this strategy was left open as an exercise in the publication. The paper was honored with the best paper award.
In spring 2004, the problem appeared in Joe Buhler and Elwyn Berlekamp's puzzle column of the quarterly The Emissary of the Mathematical Sciences Research Institute. Thereby, the authors replaced boxes by ROMs and colored strips of paper by signed numbers. The authors noted that the winning probability can be increased also in the case where the team members don't find their own numbers. If the given answer is the product of all the signs found and if the length of the longest cycle is half the (even) number of players plus one, then the team members in this cycle either all guess wrong or all guess right. Even if this extension of the strategy offers a visible improvement for a small number of players, it becomes neglibile when the number of players becomes large.
In the following years, the problem entered the mathematical literature, where it was shaped in further different ways, for example with cards on a table or wallets in lockers (locker puzzle). In the form of a prisoner problem it was posed in 2006 by Christoph Pöppe in the journal Spektrum der Wissenschaft and by Peter Winkler in the College Mathematics Journal. With slight alterations this form was adopted by Philippe Flajolet, Robert Sedgewick and Richard P. Stanley in their textbooks on combinatorics.
Empty boxes
At first, Gál and Miltersen considered in their paper the case that the number of boxes is twice the number of team members while half of the boxes are empty. This is a more difficult problem since empty boxes lead nowhere and thus the cycle-following strategy cannot be applied. It is an open problem if in this case the winning probability tends to zero with growing number of team members.
In 2005, Navin Goyal and Michael Saks developed a strategy for team B based on the cycle-following strategy for a more general problem in which the fraction of empty boxes as well as the fraction of boxes each team member is allowed to open are variable. The winning probability still tends to zero in this case, but slower than suggested by Gál and Miltersen. If the number of team members and the fraction of boxes which are opened is fixed, the winning probability stays strictly larger than zero when more empty boxes are added.
David Avis and Anne Broadbent considered in 2009 a quantum theoretical variant in which team B wins with certainty.
The malicious director
In case the prison director does not have to distribute the numbers into the drawers randomly, he can foil the prisoners' strategy if he knows the numbering of the drawers. To this end, he just has to ensure that his assignment of prisoners' numbers to drawers constitutes a permutation with a cycle of length larger than 50. The prisoners in turn can counter this by choosing their own numbering of the drawers randomly.
Monty Hall problem
In 2009, Adam S. Landsberg proposed the following simpler variant of the 100 prisoners problem which is based on the well-known Monty Hall problem:
Behind three closed doors a car, the car keys and a goat are randomly distributed. There are two players: the first player has to find the car, the second player the keys to the car. Only if both players are successful they may drive the car home. The first player enters the room and may consecutively open two of the three doors. If he is successful, the doors are closed again and the second player enters the room. The second player may also open two of the three doors, but he cannot communicate with the first player in any form. What is the winning probability if both players act optimally?If the players select their doors randomly, the winning probability is only 4/9 (about 44%). The optimal strategy is, however, as follows:
In the six possible distributions of car, keys and goat behind the three doors, the players open the following doors (in the green cases, the player was successful):
The success of the strategy is based on building a correlation between the successes and failures of the two players. Here, the winning probability is 2/3 which is optimal since the first player does not have a higher winning probability. In a further variant, three prizes are hidden behind the three doors and three players have to independently find their assigned prizes with two tries. In this case the winning probability is also 2/3 when the optimal strategy is employed.
