Data structure using c
In computer science, a data structure is a particular way of storing and organizing data in a computer so that it can be used efficiently.
Different kinds of data structures are suited to different kinds of applications, and some are highly specialized to specific tasks. For example, B-trees are particularly well-suited for implementation of databases, while compiler implementations usually use hash tables to look up identifiers.
Data structures provide a means to manage large amounts of data efficiently, such as large databases and internet indexing services. Usually, efficient data structures are a key to designing efficient algorithms. Some formal design methods and programming languages emphasize data structures, rather than algorithms, as the key organizing factor in software design. Storing and retrieving can be carried out on data stored in both main memory and in secondary memory.
Basic principles
Data structures are generally based on the ability of a computer to fetch and store data at any place in its memory, specified by an address – a bit string that can be itself stored in memory and manipulated by the program. Thus, the array and record data structures are based on computing the addresses of data items with arithmetic operations; while the linked data structures are based on storing addresses of data items within the structure itself. Many data structures use both principles, sometimes combined in non-trivial ways (as in XOR linking).
The implementation of a data structure usually requires writing a set of procedures that create and manipulate instances of that structure. The efficiency of a data structure cannot be analyzed separately from those operations. This observation motivates the theoretical concept of an abstract data type, a data structure that is defined indirectly by the operations that may be performed on it, and the mathematical properties of those operations (including their space and time cost).
TYPES OF DATA STRUCTURES
A data structure is a structured set of variables associated with one another in different ways, cooperatively defining components in the system and capable of being operated upon in the program. As stated earlier, the following operations are done on data structures:
Data organisation or clubbing
Accessing technique
Manipulating selections for information.
Data structures are the basis of programming tools and the choice of data structures should provide the following:
The data structures should satisfactorily represent the relationship between data elements.
The data structures should be easy so that the programmer can easily process the data.
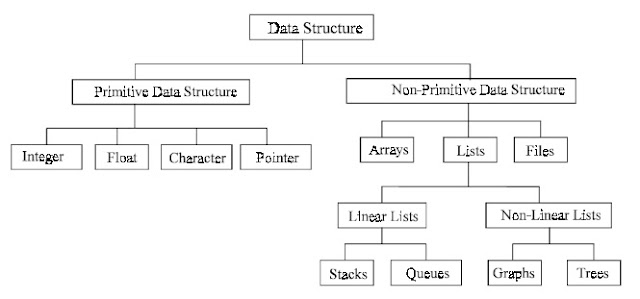
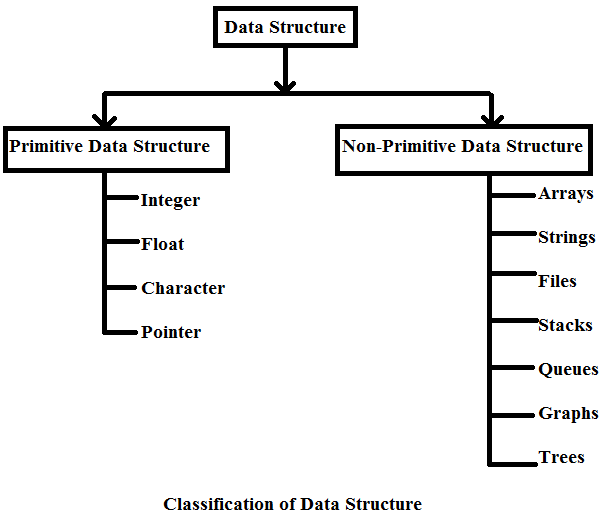
Data structures have been classified in several ways. Different authors classify it differently. Fig. 1.4 (a) shows different types of data structures. Besides these data structures some other data structures such as lattice, Petri nets, neural nets, semantic nets, search graphs, etc., can also be used. The reader can see Figs. 1.4(a) and (b) for all data structures.
Linear
In linear data structures, values are arranged in linear fashion. Arrays, linked lists, stacks and queues are examples of linear data structures in which values are stored in a sequence.
Non-Linear
This type is opposite to linear. The data values in this structure are not arranged in order. Tree, graph, table and sets are examples of non-linear data structures.
Homogenous
In this type of data structures, values of the same types of data are stored, as in an array.
Non-homogenous
In this type of data structures, data values of different types are grouped, as in structures and classes.
Dynamic
In dynamic data structures such as references and pointers, size and memory locations can be changed during program execution.
Static
Static keyword in C is used to initialize the variable to 0 (NULL). The value of a static variable remains in the memory throughout the program. Value of static variable persists. In C++ member functions are also declared as static and such functions are called as static functions and can be invoked directly.
PRIMITIVE AND NON-PRIMITIVE DATA STRUCTURES AND OPERATIONS
Primitive Data Structures
The integers, reals, logical data, character data, pointer and reference are primitive data structures. Data structures that normally are directly operated upon by machine-level instructions are known as primitive data structures.
Non-primitive Data Structures
These are more complex data structures. These data structures are derived from the primitive data structures. They stress on formation of sets of homogeneous and heterogeneous data elements.
The different operations that are to be carried out on data are nothing but designing of data structures. The various operations that can be performed on data structures.
CREATE
DESTROY
SELECT
UPDATE
An operation typically used in combination with data structures and that creates a data structure is known as creation. This operation reserves memory for the program elements. It can be carried out at compile time and run-time.
For example,
int x;
Here, variable x is declared and memory is allocated to it.
Introduction to data structure
Another operation giving the balancing effect of a creation operation is destroying operation, which destroys the data structures. The destroy operation is not an essential operation. When the program execution ends, the data structure is automatically destroyed and the memory allocated is eventually de-allocated. C++ allows the destructor member function to destroy the object. In C free () function is used to free the memory. Languages like Java have a built-in mechanism, called garbage collection, to free the memory.
The most commonly used operation linked with data structures is selection, which is used by programmers to access the data within data structures. The selection relationship depends upon yes/no. This operation updates or alters data. The other three operations associated with selections are:
Sorting
Searching
Merging
Searching operations are used to seek a particular element in the data structures. Sorting is used to arrange all the elements of data structures in the given order: either ascending or descending. There is a separate chapter on sorting and searching in this book. Merging is an operation that joins two sorted lists.
An iteration relationship is nothing but a repetitive execution of statements. For example, if we want to perform any calculation several times then iteration, in which a block of statements is repetitively executed, is useful.
One more operation used in combination with data structures is update operation. This operation changes data of data structures. An assignment operation is a good example of update operation.
For example,
int x=2;
Here, 2 is assigned to x.
x=4;
Again, 4 is reassigned to x. The value of x now is 4 because 2 is automatically replaced by 4, i.e. updated.
Stacks
In this chapter, we will study one of the most important simple data structures stack. Stack is an important tool in programming languages. Stack is one of the most essential linear data structures. Implementation of most of the system programs is based on stack data structure. We can insert or delete an element from a list, which takes place from one end. The insertion of element onto the stack is called as "push" and deletion operation is called "pop", i.e. when an item is added to the stack the operation is called "push" and when it is removed the operation is called "pop". Due to the push operation from one end, elements are added to the stack, the stack is also known as pushdown list. The most and least reachable elements in the stack are respectively known as the "top" and "bottom" of the stack. A stack is an arranged collection of elements into which new elements can be inserted or from which existing new elements can be deleted at one end. Stack is a set of elements in a last-in-first-out technique. As per Fig. the last item pushed onto the stack is always the first to be removed from the stack. The end of the stack from where the insertion or deletion operation is carried out is called top. In Fig. a stack of numbers is shown.

Queues
A queue is one of the simplest data structures and can be implemented with different methods on a computer. Queue of tasks to be executed in a computer is analogous to the queue that we see in our daily life at various places. The theory of a queue is common to all. Queue of people in a bank, students queue in school, a travellers queue for tickets at railway station are few examples of queue. It is necessary to wait in a queue for obtaining the service. In the same fashion, in a computer there may be a queue of tasks waiting for execution, few others for printing, and some are for inputting the data and instructions through the keyboard. Unless the task turns and comes on front, it will not be executed. This data structure is very useful in solving various real life problems. One can simulate the real life situations with this data structure. This chapter describes the queue and its types.

A queue is a non-primitive, linear data structure, and a sub-class of list data structure. It is an ordered, homogenous collection of elements in which elements are appended at one end called rear end and elements are deleted at other end called front end. The meaning of front is face side and rear means back side. The first entry in a queue to which the service is offered is to the element that is on front. After servicing, it is removed from the queue. The information is manipulated in the same sequence as it was collected.
TYPES OF QUEUES
In the last few topics, we have studied simple queue and already seen the disadvantages. When rear pointer reaches to the end of the queue (array), no more elements can be added in the queue, even if beginning memory locations of array are empty. To overcome the above disadvantage, different types of queues can be applied.
Circular Queue

The simple or in a straight line queue there are several limitations we know, even if memory locations at the beginning of queue are available, elements cannot be inserted as shown in the Fig. 5.9. We can efficiently utilize the space available of straight-line queue by using circular queue
APPLICATIONS OF QUEUES
There are various applications of computer science, which are performed using data structure queue. This data structure is usually used in simulation, various features of operating system, multiprogramming platform systems and different type of scheduling algorithm are implemented using queues. Round robin technique is implemented using queues. Printer server routines, various applications
Static List and Linked List
A list is a series of linearly arranged finite elements (numbers) of same type. The data elements are called nodes. The list can be of two types, i.e. basic data type or custom data type. The elements are positioned one after the other and their position numbers appear in sequence. The first element of the list is known as head and the last element is known as tail.
Searching
Searching is a technique of finding an element from the given data list or set of the elements like an array, list, or trees. It is a technique to find out an element in a sorted or unsorted list. For example, consider an array of 10 elements. These data elements are stored in successive memory locations. We need to search an element from the array. In the searching operation, assume a particular element n is to be searched. The element n is compared with all the elements in a list starting from the first element of an array till the last element. In other words, the process of searching is continued till the element is found or list is completely exhausted. When the exact match is found then the search process is terminated. In case, no such element exists in the array, the process of searching should be abandoned.
LINEAR (SEQUENTIAL) SEARCH
The linear search is a conventional method of searching data. The linear search is a method of searching a target element in a list sequence. The expected element is to be searched in the entire data structure in a sequential method from starting to last element. Though, it is simple and straightforward, it has serious limitations. It consumes more time and reduces the retrieval rate of the system. The linear or sequential name implies that the items are stored in systematic manner. The linear search can be applied on sorted or unsorted linear data structure.
BINARY SEARCH

The binary search approach is different from the linear search. Here, search of an element is not passed in sequence as in the case of linear search. Instead, two partitions of lists are made and then the given element is searched. Hence, it creates two parts of the lists known as binary search.
Binary search is quicker than the linear search. It is an efficient searching technique and works with sorted lists. However, it cannot be applied on unsorted data structure. Before applying binary search, the linear data structure must be sorted in either ascending or descending order. The binary search is unsuccessful if the elements are unordered. The binary search is based on the approach divide-and-conquer. In binary search, the element is compared with the middle element. If the expected element falls before the middle element, the left portion is searched otherwise right portion is searched.
Sorting
In real life we come across several examples of sorted information. For example, in telephone directory the names of the subscribers and their phone numbers are written in alphabetial order. The records of the list of these telephone holders are to be sorted by their names. By using this directory, we can access the telephone number and address of the subscriber very easily.
Bankers or businesspersons sort the currency denomination notes received from customers in the appropriate form. Currency denominations of Rs 1000, 500, 100, 50, 20, 10, 5, and 1 are separated first and then separate bundles are prepared.
INSERTION SORT
In insertion sort the element is inserted at appropriate place. For example, consider an array of n elements. In this type, swapping of elements is done without taking any temporary variable. The greater numbers are shifted towards the end of the array and smaller are shifted to beginning. Here, a real life example of playing cards can be cited. We keep the cards in increasing order. The card having least value is placed at the extreme left and the largest one at the other side. In between them the other cards are managed in ascending order.
SELECTION SORT
The selection sort is nearly the same as exchange sort. Assume, we have a list containing n elements. By applying selection sort, the first element is compared with all remaining (n-1) elements. The smallest element is placed at the first location. Again, the second element is compared with remaining (n-2) elements. If the item found is lesser than the compared elements in the remaining (n-2) list then the swap operation is done. In this type, entire array is checked for the smallest element and then swapped.
BUBBLE SORT
Bubble sort is a commonly used sorting algorithm. In this type, two successive elements are compared and swapping is done if the first element is greater than the second one. The elements are sorted in ascending order. It is easy to understand but it is time consuming.
Bubble sort is an example of exchange sort. In this method repetitively comparison is performed between the two successive elements and if essential swapping of elements is done. Thus, step-by-step entire array elements are checked. It is different from the selection sort. Instead of searching the minimum element and then applying swapping, two records are swapped instantly upon noticing that they are not in order.
QUICK SORT
It is also known as partition exchange sort. It was invented by CAR Hoare. It is based on partition. Hence, the method falls under divide and conquer technique. The main list of elements is divided into two sub-lists. For example, a list of X elements are to be sorted. The quick sort marks an element in a list called as pivot or key. Consider the first element J as a pivot. Shift all the elements whose value is less than J towards the left and elements whose value is greater than J to the right of J. Now, the key element divides the main list into two parts. It is not necessary that selected key element must be in the middle. Any element from the list can act as key element. However, for best performance preference is given to middle elements. Time consumption of the quick sort depends on the location of the key in the list.
MERGING LIST
Merging is a process in which two lists are merged to form a new list. The new list is the sorted list. Before merging, individual lists are sorted and then merging is done. The procedure is very straightforward.
RADIX SORT
The radix sort is a technique, which is based on the position of digits. The number is represented with different positions. The number has units, tens, hundreds positions onwards. Based on its position the sorting is done. For example, consider the number 456, which is selected for sorting. In this number 6 is at units position and 5 is at tens and 4 is at the hundreds position. 3 passes would be needed for the sorting of this number with this procedure. In the first pass, we place all numbers at the unit place. In the second pass all numbers are placed in the list with consents to the tens position digit value. Also, in the third pass the numbers are placed with consent to the value of the hundreds position digit.
Trees
BASIC TERMS
Some of the basic concepts relevant to trees are described in this section. These are node, parents, roots, child, link, leaf, level, height, degree of node, sibling, terminal nodes, path length, and forest.
BINARY TREES
A binary tree is a finite set of data elements. A tree is binary if each node of it has a maximum of two branches. The data element is either empty or holds a single element called root along with two disjoint trees called left sub-tree and right sub-tree, i.e. in a binary tree the maximum degree of any node is two. The binary tree may be empty. However, the tree cannot be empty. The node of tree can have any number of children whereas the node of binary tree can have maximum two children. Fig. shows a sample binary tree.

BINARY SEARCH TREE
A binary search tree is also called as binary sorted tree. Binary search tree is either empty or each node N of tree satisfies the following property:
The key value in the left child is not more than the value of root.
The key value in the right child is more than or identical to the value of root.
All the sub-trees, i.e. left and right sub-trees follow the two rules mentioned above.
BINARY TREE REPRESENTATION
Binary tree can be represented by two ways:
Array representation
Linked representation.
Graph
Graphs are frequently used in every walk of life. Every day we come across various kinds of graphs appearing in newspapers or television. The countries in a globe are seen in a map. A map depends on the geographic location of the places or cities. As such, a map is a well-known example of a graph. In the map, various connections are shown between the cities. The cities are connected via roads, rail or aerial network. How to reach a place is indicated by means of a graph.
GRAPH
A graph is set of nodes and arcs. The nodes are also termed as vertices and arcs are termed as edges. The set of nodes as per the Graph can be represented as,
G= (V,E) and V(G)= (O, Q, P, R, S) or group of vertices.
GRAPH REPRESENTATION
The graph can be implemented by linked list or array. Fig. illustrates a graph and its representation and implementation is also described.
refer this site for detailed knowledge
In computer science, a data structure is a particular way of storing and organizing data in a computer so that it can be used efficiently.
Different kinds of data structures are suited to different kinds of applications, and some are highly specialized to specific tasks. For example, B-trees are particularly well-suited for implementation of databases, while compiler implementations usually use hash tables to look up identifiers.
Data structures provide a means to manage large amounts of data efficiently, such as large databases and internet indexing services. Usually, efficient data structures are a key to designing efficient algorithms. Some formal design methods and programming languages emphasize data structures, rather than algorithms, as the key organizing factor in software design. Storing and retrieving can be carried out on data stored in both main memory and in secondary memory.
Basic principles
Data structures are generally based on the ability of a computer to fetch and store data at any place in its memory, specified by an address – a bit string that can be itself stored in memory and manipulated by the program. Thus, the array and record data structures are based on computing the addresses of data items with arithmetic operations; while the linked data structures are based on storing addresses of data items within the structure itself. Many data structures use both principles, sometimes combined in non-trivial ways (as in XOR linking).
The implementation of a data structure usually requires writing a set of procedures that create and manipulate instances of that structure. The efficiency of a data structure cannot be analyzed separately from those operations. This observation motivates the theoretical concept of an abstract data type, a data structure that is defined indirectly by the operations that may be performed on it, and the mathematical properties of those operations (including their space and time cost).
TYPES OF DATA STRUCTURES
A data structure is a structured set of variables associated with one another in different ways, cooperatively defining components in the system and capable of being operated upon in the program. As stated earlier, the following operations are done on data structures:

Data organisation or clubbing
Accessing technique
Manipulating selections for information.
Data structures are the basis of programming tools and the choice of data structures should provide the following:
The data structures should satisfactorily represent the relationship between data elements.
The data structures should be easy so that the programmer can easily process the data.
Data structures have been classified in several ways. Different authors classify it differently. Fig. 1.4 (a) shows different types of data structures. Besides these data structures some other data structures such as lattice, Petri nets, neural nets, semantic nets, search graphs, etc., can also be used. The reader can see Figs. 1.4(a) and (b) for all data structures.
Linear
In linear data structures, values are arranged in linear fashion. Arrays, linked lists, stacks and queues are examples of linear data structures in which values are stored in a sequence.
Non-Linear
This type is opposite to linear. The data values in this structure are not arranged in order. Tree, graph, table and sets are examples of non-linear data structures.
Homogenous
In this type of data structures, values of the same types of data are stored, as in an array.
Non-homogenous
In this type of data structures, data values of different types are grouped, as in structures and classes.
Dynamic
In dynamic data structures such as references and pointers, size and memory locations can be changed during program execution.
Static
Static keyword in C is used to initialize the variable to 0 (NULL). The value of a static variable remains in the memory throughout the program. Value of static variable persists. In C++ member functions are also declared as static and such functions are called as static functions and can be invoked directly.
PRIMITIVE AND NON-PRIMITIVE DATA STRUCTURES AND OPERATIONS

Primitive Data Structures
The integers, reals, logical data, character data, pointer and reference are primitive data structures. Data structures that normally are directly operated upon by machine-level instructions are known as primitive data structures.
Non-primitive Data Structures
These are more complex data structures. These data structures are derived from the primitive data structures. They stress on formation of sets of homogeneous and heterogeneous data elements.
The different operations that are to be carried out on data are nothing but designing of data structures. The various operations that can be performed on data structures.
CREATE
DESTROY
SELECT
UPDATE
An operation typically used in combination with data structures and that creates a data structure is known as creation. This operation reserves memory for the program elements. It can be carried out at compile time and run-time.
For example,
int x;
Here, variable x is declared and memory is allocated to it.
Introduction to data structure
Another operation giving the balancing effect of a creation operation is destroying operation, which destroys the data structures. The destroy operation is not an essential operation. When the program execution ends, the data structure is automatically destroyed and the memory allocated is eventually de-allocated. C++ allows the destructor member function to destroy the object. In C free () function is used to free the memory. Languages like Java have a built-in mechanism, called garbage collection, to free the memory.
The most commonly used operation linked with data structures is selection, which is used by programmers to access the data within data structures. The selection relationship depends upon yes/no. This operation updates or alters data. The other three operations associated with selections are:
Sorting
Searching
Merging
Searching operations are used to seek a particular element in the data structures. Sorting is used to arrange all the elements of data structures in the given order: either ascending or descending. There is a separate chapter on sorting and searching in this book. Merging is an operation that joins two sorted lists.
An iteration relationship is nothing but a repetitive execution of statements. For example, if we want to perform any calculation several times then iteration, in which a block of statements is repetitively executed, is useful.
One more operation used in combination with data structures is update operation. This operation changes data of data structures. An assignment operation is a good example of update operation.
For example,
int x=2;
Here, 2 is assigned to x.
x=4;
Again, 4 is reassigned to x. The value of x now is 4 because 2 is automatically replaced by 4, i.e. updated.
Stacks
In this chapter, we will study one of the most important simple data structures stack. Stack is an important tool in programming languages. Stack is one of the most essential linear data structures. Implementation of most of the system programs is based on stack data structure. We can insert or delete an element from a list, which takes place from one end. The insertion of element onto the stack is called as "push" and deletion operation is called "pop", i.e. when an item is added to the stack the operation is called "push" and when it is removed the operation is called "pop". Due to the push operation from one end, elements are added to the stack, the stack is also known as pushdown list. The most and least reachable elements in the stack are respectively known as the "top" and "bottom" of the stack. A stack is an arranged collection of elements into which new elements can be inserted or from which existing new elements can be deleted at one end. Stack is a set of elements in a last-in-first-out technique. As per Fig. the last item pushed onto the stack is always the first to be removed from the stack. The end of the stack from where the insertion or deletion operation is carried out is called top. In Fig. a stack of numbers is shown.

Queues
A queue is one of the simplest data structures and can be implemented with different methods on a computer. Queue of tasks to be executed in a computer is analogous to the queue that we see in our daily life at various places. The theory of a queue is common to all. Queue of people in a bank, students queue in school, a travellers queue for tickets at railway station are few examples of queue. It is necessary to wait in a queue for obtaining the service. In the same fashion, in a computer there may be a queue of tasks waiting for execution, few others for printing, and some are for inputting the data and instructions through the keyboard. Unless the task turns and comes on front, it will not be executed. This data structure is very useful in solving various real life problems. One can simulate the real life situations with this data structure. This chapter describes the queue and its types.

A queue is a non-primitive, linear data structure, and a sub-class of list data structure. It is an ordered, homogenous collection of elements in which elements are appended at one end called rear end and elements are deleted at other end called front end. The meaning of front is face side and rear means back side. The first entry in a queue to which the service is offered is to the element that is on front. After servicing, it is removed from the queue. The information is manipulated in the same sequence as it was collected.
TYPES OF QUEUES
In the last few topics, we have studied simple queue and already seen the disadvantages. When rear pointer reaches to the end of the queue (array), no more elements can be added in the queue, even if beginning memory locations of array are empty. To overcome the above disadvantage, different types of queues can be applied.
Circular Queue

The simple or in a straight line queue there are several limitations we know, even if memory locations at the beginning of queue are available, elements cannot be inserted as shown in the Fig. 5.9. We can efficiently utilize the space available of straight-line queue by using circular queue
APPLICATIONS OF QUEUES
There are various applications of computer science, which are performed using data structure queue. This data structure is usually used in simulation, various features of operating system, multiprogramming platform systems and different type of scheduling algorithm are implemented using queues. Round robin technique is implemented using queues. Printer server routines, various applications
Static List and Linked List
A list is a series of linearly arranged finite elements (numbers) of same type. The data elements are called nodes. The list can be of two types, i.e. basic data type or custom data type. The elements are positioned one after the other and their position numbers appear in sequence. The first element of the list is known as head and the last element is known as tail.
Searching
Searching is a technique of finding an element from the given data list or set of the elements like an array, list, or trees. It is a technique to find out an element in a sorted or unsorted list. For example, consider an array of 10 elements. These data elements are stored in successive memory locations. We need to search an element from the array. In the searching operation, assume a particular element n is to be searched. The element n is compared with all the elements in a list starting from the first element of an array till the last element. In other words, the process of searching is continued till the element is found or list is completely exhausted. When the exact match is found then the search process is terminated. In case, no such element exists in the array, the process of searching should be abandoned.
LINEAR (SEQUENTIAL) SEARCH
The linear search is a conventional method of searching data. The linear search is a method of searching a target element in a list sequence. The expected element is to be searched in the entire data structure in a sequential method from starting to last element. Though, it is simple and straightforward, it has serious limitations. It consumes more time and reduces the retrieval rate of the system. The linear or sequential name implies that the items are stored in systematic manner. The linear search can be applied on sorted or unsorted linear data structure.
BINARY SEARCH

The binary search approach is different from the linear search. Here, search of an element is not passed in sequence as in the case of linear search. Instead, two partitions of lists are made and then the given element is searched. Hence, it creates two parts of the lists known as binary search.
Binary search is quicker than the linear search. It is an efficient searching technique and works with sorted lists. However, it cannot be applied on unsorted data structure. Before applying binary search, the linear data structure must be sorted in either ascending or descending order. The binary search is unsuccessful if the elements are unordered. The binary search is based on the approach divide-and-conquer. In binary search, the element is compared with the middle element. If the expected element falls before the middle element, the left portion is searched otherwise right portion is searched.
Sorting
In real life we come across several examples of sorted information. For example, in telephone directory the names of the subscribers and their phone numbers are written in alphabetial order. The records of the list of these telephone holders are to be sorted by their names. By using this directory, we can access the telephone number and address of the subscriber very easily.
Bankers or businesspersons sort the currency denomination notes received from customers in the appropriate form. Currency denominations of Rs 1000, 500, 100, 50, 20, 10, 5, and 1 are separated first and then separate bundles are prepared.
INSERTION SORT
In insertion sort the element is inserted at appropriate place. For example, consider an array of n elements. In this type, swapping of elements is done without taking any temporary variable. The greater numbers are shifted towards the end of the array and smaller are shifted to beginning. Here, a real life example of playing cards can be cited. We keep the cards in increasing order. The card having least value is placed at the extreme left and the largest one at the other side. In between them the other cards are managed in ascending order.
SELECTION SORT
The selection sort is nearly the same as exchange sort. Assume, we have a list containing n elements. By applying selection sort, the first element is compared with all remaining (n-1) elements. The smallest element is placed at the first location. Again, the second element is compared with remaining (n-2) elements. If the item found is lesser than the compared elements in the remaining (n-2) list then the swap operation is done. In this type, entire array is checked for the smallest element and then swapped.
BUBBLE SORT
Bubble sort is a commonly used sorting algorithm. In this type, two successive elements are compared and swapping is done if the first element is greater than the second one. The elements are sorted in ascending order. It is easy to understand but it is time consuming.
Bubble sort is an example of exchange sort. In this method repetitively comparison is performed between the two successive elements and if essential swapping of elements is done. Thus, step-by-step entire array elements are checked. It is different from the selection sort. Instead of searching the minimum element and then applying swapping, two records are swapped instantly upon noticing that they are not in order.
It is also known as partition exchange sort. It was invented by CAR Hoare. It is based on partition. Hence, the method falls under divide and conquer technique. The main list of elements is divided into two sub-lists. For example, a list of X elements are to be sorted. The quick sort marks an element in a list called as pivot or key. Consider the first element J as a pivot. Shift all the elements whose value is less than J towards the left and elements whose value is greater than J to the right of J. Now, the key element divides the main list into two parts. It is not necessary that selected key element must be in the middle. Any element from the list can act as key element. However, for best performance preference is given to middle elements. Time consumption of the quick sort depends on the location of the key in the list.
MERGING LIST
Merging is a process in which two lists are merged to form a new list. The new list is the sorted list. Before merging, individual lists are sorted and then merging is done. The procedure is very straightforward.
RADIX SORT
The radix sort is a technique, which is based on the position of digits. The number is represented with different positions. The number has units, tens, hundreds positions onwards. Based on its position the sorting is done. For example, consider the number 456, which is selected for sorting. In this number 6 is at units position and 5 is at tens and 4 is at the hundreds position. 3 passes would be needed for the sorting of this number with this procedure. In the first pass, we place all numbers at the unit place. In the second pass all numbers are placed in the list with consents to the tens position digit value. Also, in the third pass the numbers are placed with consent to the value of the hundreds position digit.
Trees
BASIC TERMS
Some of the basic concepts relevant to trees are described in this section. These are node, parents, roots, child, link, leaf, level, height, degree of node, sibling, terminal nodes, path length, and forest.
BINARY TREES
A binary tree is a finite set of data elements. A tree is binary if each node of it has a maximum of two branches. The data element is either empty or holds a single element called root along with two disjoint trees called left sub-tree and right sub-tree, i.e. in a binary tree the maximum degree of any node is two. The binary tree may be empty. However, the tree cannot be empty. The node of tree can have any number of children whereas the node of binary tree can have maximum two children. Fig. shows a sample binary tree.

BINARY SEARCH TREE
A binary search tree is also called as binary sorted tree. Binary search tree is either empty or each node N of tree satisfies the following property:
The key value in the left child is not more than the value of root.
The key value in the right child is more than or identical to the value of root.
All the sub-trees, i.e. left and right sub-trees follow the two rules mentioned above.
BINARY TREE REPRESENTATION
Binary tree can be represented by two ways:
Array representation
Linked representation.
Graph
Graphs are frequently used in every walk of life. Every day we come across various kinds of graphs appearing in newspapers or television. The countries in a globe are seen in a map. A map depends on the geographic location of the places or cities. As such, a map is a well-known example of a graph. In the map, various connections are shown between the cities. The cities are connected via roads, rail or aerial network. How to reach a place is indicated by means of a graph.
GRAPH
A graph is set of nodes and arcs. The nodes are also termed as vertices and arcs are termed as edges. The set of nodes as per the Graph can be represented as,
G= (V,E) and V(G)= (O, Q, P, R, S) or group of vertices.
GRAPH REPRESENTATION
The graph can be implemented by linked list or array. Fig. illustrates a graph and its representation and implementation is also described.
refer this site for detailed knowledge
.jpg)