
Automata theory is the study of abstract machines and automata, as well as the computational problems that can be solved using them. It is a theory in theoretical computer science, under Discrete mathematics (a section of Mathematics and also of Computer Science). Automata comes from the Greek word ???????? meaning "self-acting".
So, Automata Theory is the study of self-operating virtual machines to help in logical understanding of input and output process, without or with intermediate stage(s) of computation (or any function / process).

The figure at right illustrates a finite state machine, which belongs to one well-known variety of automaton. This automaton consists of states (represented in the figure by circles), and transitions (represented by arrows). As the automaton sees a symbol of input, it makes a transition (or jump) to another state, according to its transition function (which takes the current state and the recent symbol as its inputs).
Automata theory is also closely related to formal language theory. An automaton is a finite representation of a formal language that may be an infinite set. Automata are often classified by the class of formal languages they are able to recognize.
Automata play a major role in theory of computation, compiler design, artificial intelligence, parsing and formal verification.
refer this site for more information
http://gr12computers.wikispaces.com/Automata+Theory
Introduction and Finite Automata
A finite automaton (FA) is a simple idealized machine used to recognize patterns within input taken from some character set (or alphabet) C. The job of an FA is to accept or reject an input depending on whether the pattern defined by the FA occurs in the input.
A finite automaton consists of:
1. a finite set S of N states
2. a special start state
3. a set of final (or accepting) states
4. a set of transitions T from one state to another, labeled with chars in C
As noted above, we can represent a FA graphically, with nodes for states, and arcs for transitions.
We execute our FA on an input sequence as follows:
1. Begin in the start state
2. If the next input char matches the label on a transition from the current state to a new state, go to that new state
3. Continue making transitions on each input char
4. If no move is possible, then stop
5. If in accepting state, then accept
Alphabet
An alphabet is a set of characters. For instance, A = {a, b, c} is a possible alphabet, and so is 2 = {0, 1}, and so is the English alphabet which has all letters, numbers, signs, punctuations, etc.
(If you’re wondering what the hell characters are from a set-theoretic perspective, they’re just other sets - I have proved that the alphabet {0, 1} has the same power as any other alphabets so you can just define other characters as strings of 0s and 1s.)
From an alphabet we can generate strings. A string is an ordered sequence of characters. ‘abbabcabacc’ is a valid string on the alphabet A defined above, and ‘00101011’ is a valid string on the alphabet {0, 1} defined above. Every alphabet has a special string ? called the empty string which is a string with no characters. (From a set-theoretic perspective, we can just say that a string with n characters is an ordered n-tuple and be done with it. The specific formulation isn’t important.)
We have also a binary operation called string concatenation which we will represent by x + y or xy interchangeably given two strings x and y. Basically, if we concatenate two strings, we place one string at the end of the other. The concatenation of the string ‘alpha’ and ‘bet’ is ‘alphabet’ (or ‘betalpha’ depending on the order you want).
Language
A language on the alphabet A is a subset of A*, or equivalently a member of P(A*) (the powerset of A*). Any subsets of the Kleene closure of an alphabet can be considered languages, but the vast majority of them aren’t useful (since there are, in fact, uncountably many languages on any finite alphabet because the set of all languages on A is given by P(A*)). The useful languages generally have rules.
One possible rule of a language on the alphabet A = {a, b, c} is that only the string ‘abc’ is a member of that language. All other strings aren’t. But we needn’t be so uncreative. We generally have symbols to talk about languages. I’ll give you an example of a language on A:
L = ab*(c|a)b
This language accepts all strings that start with an a, are followed by any number (possibly 0) of bs, then by ether a c or an a, then end with a b. From the following list, which strings belong to L?
abbcb
abbb
bbb
aabbbab
abbbab
acb
bbcb
aab
abbbbbbbcab
abbbbcb
The strings number 1, 5, 6, 8 and 10 belong to the language L. We give other examples of languages:
L = ab(a|b|c)*
L = b*
L = baab(baab)*bc
L = anbn
L = anbncn
Can you explain what strings are accepted by each language?
1. The first accepts all strings that start with ab. After ab, any number of any other characters, even 0, can be accepted.
2. The second one accepts strings composed entirely of the character b and the empty string.
3. The third accepts a string that starts with baab, then repeats baab any number of times (including 0), then ends with bc. Usually, when we want to repeat a string any nonzero number of times we use the notation x+, but I decided against it to not confuse you.
4. The fourth one accepts any strings that have a certain number of as followed by the same number of bs.
5. The fifth and final one accepts any strings that have a certain number of as followed by the same number of bs followed by the same number of cs.
Deterministic Finite Automata (DFA)

In automata theory, a branch of theoretical computer science, a deterministic finite automaton (DFA)—also known as deterministic finite state machine—is a finite state machine that accepts/rejects finite strings of symbols and only produces a unique computation (or run) of the automaton for each input string. Deterministic refers to the uniqueness of the computation. In search of simplest models to capture the finite state machines, McCulloch and Pitts were among the first researchers to introduce a concept similar to finite automaton in 1943.
A DFA is defined as an abstract mathematical concept, but due to the deterministic nature of a DFA, it is implementable in hardware and software for solving various specific problems. For example, a DFA can model software that decides whether or not online user-input such as email addresses are valid.
DFAs recognize exactly the set of regular languages which are, among other things, useful for doing lexical analysis and pattern matching. DFAs can be built from nondeterministic finite automata (NFAs) using the powerset construction method.
Nondeterministic finite automaton(NFA)
n automata theory, a nondeterministic finite automaton (NFA), or nondeterministic finite state machine, is a finite state machine that (1) does not require input symbols for state transitions and (2) is capable of transitioning to zero or two or more states for a given start state and input symbol. This distinguishes it from a deterministic finite automaton (DFA), in which all transitions are uniquely determined and in which an input symbol is required for all state transitions. Although NFA and DFA have distinct definitions, all NFAs can be translated to equivalent DFAs using the subset construction algorithm, i.e., constructed DFAs and their corresponding NFAs recognize the same formal language. Like DFAs, NFAs only recognize regular languages.
NFAs were introduced in 1959 by Michael O. Rabin and Dana Scott, who also showed their equivalence to DFAs.
NFAs have been generalized in multiple ways, e.g., nondeterministic finite automaton with ?-moves, pushdown automaton, ?-automaton, and probabilistic automata.
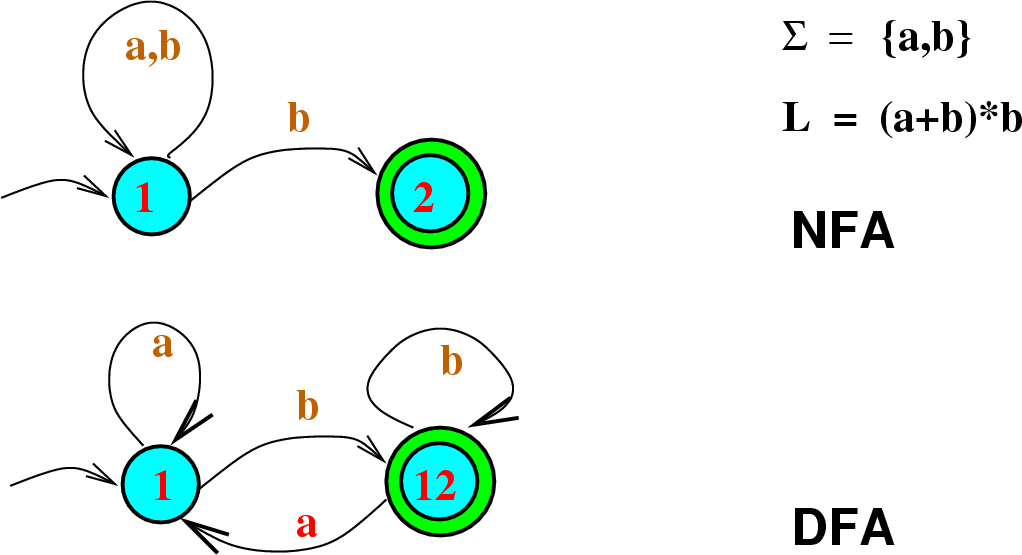
An NFA, similar to a DFA, consumes a string of input symbols. For each input symbol, it transitions to a new state until all input symbols have been consumed. Unlike a DFA, it is non-deterministic, i.e., for some state and input symbol, the next state may be one of two or more possible states. Thus, in the formal definition, the next state is an element of the power set of the states, which is a set of states to be considered at once. The notion of accepting an input is similar to that for the DFA. When the last input symbol is consumed, the NFA accepts if and only if there is some set of transitions that will take it to an accepting state. Equivalently, it rejects, if, no matter what transitions are applied, it would not end in an accepting state.
NFA to DFA conversion
Let M2 = < Q2 ,
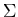 ,
q2,0 ,
,
q2,0 , 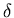 2 , A2 > be an
NFA
that recognizes a language L.
Then the DFA M
= < Q,
2 , A2 > be an
NFA
that recognizes a language L.
Then the DFA M
= < Q, 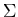 ,
q0 ,
,
q0 , 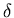 , A > that satisfies the following conditions recognizes L:
, A > that satisfies the following conditions recognizes L:
Q = 2Q2 , that is the set of all subsets of Q2 ,
q0 = { q2,0 } ,
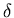 ( q, a ) =
( q, a ) =  for each state q in Q and each symbol a in
for each state q in Q and each symbol a in 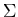 and
and
A = { q
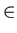 Q | q
Q | q 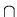 A2
A2
 }
}
To obtain a DFA M = < Q,
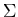 ,
q0 ,
,
q0 , 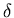 , A > which accepts the same language as the given
NFA
M2 = < Q2 ,
, A > which accepts the same language as the given
NFA
M2 = < Q2 , 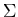 ,
q2,0 ,
,
q2,0 , 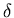 2 , A2 > does,
you may proceed as follows:
2 , A2 > does,
you may proceed as follows:
Initially Q =
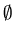 .
.
First put { q2,0 } into Q. { q2,0 } is the initial state of the DFA M.
Then for each state q in Q do the following:
add the set
 , where
, where 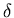 here is that of NFA M2,
as a state to Q if it is not already in Q for each symbol a
in
here is that of NFA M2,
as a state to Q if it is not already in Q for each symbol a
in 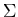 .
.
For this new state, add
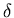 ( q, a ) =
( q, a ) =
 to
to
 , where the
, where the 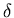 on the right hand side
is that of NFA M2.
on the right hand side
is that of NFA M2.
When no more new states can be added to Q, the process terminates. All the states of Q that contain accepting states of M2 are accepting states of M.
The states that are not reached from the initial state are not included in Q obtained by this procedure. Thus the set of states Q thus obtained is not necessarily equal to 2Q2 .
minimization of FSM
Problems associated with constructing and minimizing finite state machines arise repeatedly in software and hardware design applications. Finite state machines are best thought of as pattern recognizers, and minimum-size machines correspond to recognizers that require less time and space. Complicated control systems and compilers are often built using finite state machines to encode the current state and associated actions, as well as the set of possible transitions to other states. Minimizing the size of this machine minimizes its cost.
Finite state machines are best thought of as edge-labeled directed graphs, where each vertex represents one of n states and each edge a transition from one state to the other on receipt of the alphabet symbol that labels the edge. The automaton above analyzes a given sequence of coin tosses, with the dark states signifying that an even number of heads have been observed. Automata can be represented using any graph data structure (see Section gif), or by using an tex2html_wrap_inline30998 transition matrix, where tex2html_wrap_inline31000 is the size of the alphabet.
Finite state machines are often used to specify search patterns in the guise of regular expressions, which are patterns formed by and-ing, or-ing, and looping over smaller regular expressions. For example, the regular expression tex2html_wrap_inline31002 matches any string on (a,b,c) that begins and ends with an a (including a itself). The best way to test whether a string is described by a given regular expression (especially if many strings will be tested) is to construct the equivalent finite automaton and then simulate the machine on the string. See Section gif for alternative approaches to string matching.
We consider three different problems on finite automata:
1. Minimizing deterministic finite state machines - Transition matrices for finite automata quickly become prohibitively large for sophisticated machines, thus fueling the need for tighter encodings. The most direct approach is to eliminate redundant states in the automaton. As the example above illustrates, automata of widely varying sizes can compute the same function.
2. Algorithms for minimizing the number of states in a deterministic finite automaton (DFA) appear in any book on automata theory. The basic approach works by partitioning the states into gross equivalence classes and then refining the partition. Initially, the states are partitioned into accepting, rejecting, and other classes. The transitions from each node branch to a given class on a given symbol. Whenever two states , t in the same class C branch to elements of different classes, the class C must be partitioned into two subclasses, one containing , the other containing t.
3. This algorithm makes a sweep though all the classes looking for a new partition, and repeating the process from scratch if it finds one. This yields an tex2html_wrap_inline31006 algorithm, since at most n-1 sweeps need ever be performed. The final equivalence classes correspond to the states in the minimum automaton. In fact, a more efficient, tex2html_wrap_inline31008 algorithm is known with available implementations discussed below.
4. Constructing deterministic machines from nondeterministic machines - DFAs are simple to understand and work with, because the machine is always in exactly one state at any given time. Nondeterministic automata (NFAs) can be in more than one state at a time, so its current ``state represents a subset of all possible machine states.
5. In fact, any NFA can be mechanically converted to an equivalent DFA, which can then be minimized as above. However, converting an NFA to a DFA can cause an exponential blowup in the number of states, which perversely might later be eliminated in the minimization. This exponential blowup makes automaton minimization problems NP-hard whenever you do not start with a DFA.
6. The proofs of equivalence between NFAs, DFAs, and regular expressions are elementary enough to be covered in undergraduate automata theory classes. However, they are surprisingly nasty to implement, for reasons including but not limited to the exponential blowup of states. Implementations are discussed below.
7. Constructing machines from regular expressions - There are two approaches to converting a regular expression to an equivalent finite automaton, the difference being whether the output automaton is to be a nondeterministic or deterministic machine. The former is easier to construct but less efficient to simulate.
Finite Automata with output- Moore and Mealy machines.
Finite Automata with output- Moore and Mealy machines.
If a combinational logic circuit is an implementation of a Boolean function, then a sequential logic circuit can be considered an implementation of a finite state machine. There is a little more to it than that (because a sequential logic circuit can contain combinational logic circuits).
If you take a course in programming languages, you will also learn about finite state machines. Usually, you will call it a DFA (deterministic finite automata).
While finite state machines with outputs are essentially DFAs, the purpose behind them is different.
DFAs in programming languages
When you are learning about models of computation, one simple model is a deterministic finite automata or DFA for short.
Formally, the definition of a DFA is:
Q, a set of states
S, an single state which is an element of Q. This is the start state.
F, a set of states designated as the final states
Sigma, the input alphabet
delta, a transition function that maps a state and a letter from the input alphabet, to a state
DFAs are used to recognize a language, L. A language is a set of strings made from characters in the input alphabet. If a language can be recognized by a DFA, it is said to have a regular grammar.
To use a DFA, you start in an initial state, and process the input string a character at a time. For example, if the input alphabet consists of "a" and "b", then a typical question is to ask whether the string "aaab" is accepted by a DFA.

To find out whether it is accepted, you start off in the state state, S. Then you process each character (first "a", then "a", then "a", and finally "b"). This may cause you to move from one state to another. After the last character is processed, if you are in a final state, then the string is in the language. Otherwise, its not in the language.
There are some languages that cant be recognized by a DFA (for example, palindromes). Thus, a DFA, while reasonably powerful, there are other (mathematical) machines that are more powerful.
Often, tokens in programming languages can be described using a regular grammar.
FSM with output in hardware
A finite state machine with output is similar to describe formally.
Q, a set of states
S, an single state which is an element of Q. This is the start state.
Sigma, the input alphabet
Pi, the output alphabet
delta, a transition function that maps a state and a letter from the input alphabet, to a state and a letter from the output alphabet.
The primary difference is that there is no set of final states, and that the transition function not only puts you in a new state, but also generates an output symbol.
The goal of this kind of FSM is not accepting or rejecting strings, but generating a set of outputs given a set of inputs. Recall that a black box takes in inputs, processes, and generates outputs. FSMs are one way of describing how the inputs are being processed, based on the inputs and state, to generate outputs. Thus, were very interested in what output is generated.
In DFAs, we dont care what output is generated. We care only whether a string has been accepted by the DFA or not.
Since were talking about circuits, the input alphabet is going to be the set of k bit bitstrings, while the output alphabet is the set of m bit bitstrings.
FSM with Outputs: Moore machines
The goal of FSMs is to describe a circuit with inputs and outputs. So far, we have inputs, that tell us which state we should go to, given some initial, start state. However, the machine generates no outputs.
We modify the FSM shown above, by adding outputs. Moore machines add outputs to each state. Thus, each state is associated with an output. When you transition into the state, the output corresponding to the state is produced. The information in the state is typically written as 01/1. 01 indicates the state, while 1 indicates the output. 01/1 is short hand for q1q0 = 01/z = 1
The number of bits in the output is arbitary, and depends on whatever your application needs. Thus, the number of bits may be less than, equal, or greater than the number of bits used to represent the state.
FSM with Outputs: Mealy machines
A Moore machine has outputs that are a function of state. That is, z = f( qk-1,..., q0 ).
A Mealy machine has outputs that are a function of state and input, that is That is, z = f( qk-1,..., q0, xm-1,..., x0 ).
We usually indicate that the output is depedent on current state and input by drawing the output on the edge. In the example below, look at the edge from state 00 to state 01. This edge has the value 1/1. This means, that if you are in state 00, and you see an input of 1, then you output a 1, and transition to state 01.
Thus, 1/1 is short hand for x = 1 / z = 1.
Equivalence of Mealy and Moore machines
We have two ways to describe a FSM: Mealy and Moore machines. A mathematician might ask: are the two machines equivalent?
Initially, you might think not. A Mealy machine can have its output depend on both input and state. Thus, if we ignore the state, we should be able to convert a Moore machine to a Mealy machine.
Its not so easy to see that you can convert an arbitrary Mealy machine to a Moore machine.
It turns out that the two machines are equivalent. What does that mean? It means that given a Moore machine, you can create a Mealy machine, such that if both machines are fed the same sequence of inputs, they will both produce the same sequence of outputs. You can also convert from a Mealy machine to its equivalent Moore machine, and again generate the same outputs given the same sequence of inputs.
Actually, to be precise we must ignore one fact about Moore machines. Moore machines generate output even if no input has been read in. So, if you ignore this initial output of the Moore machine, you can convert between one machine and the other.
The actual algorithm is beyond the scope of the course. However, the basic idea of converting a Mealy machine to a Moore machine is to increase the number of states. Roughly speaking, if you have a Mealy machine with N states, and there are k bits of input, you may need up to 2kN states in the equivalent Moore machine.Effectively, the new states record information about how that state was reached.
FA and Regular Expressions
This section specifically describes how one may transform any finite automaton into a regular expression by using the tools under the “Convert ? Convert FA to RE” menu option. For knowledge of many of the general tools, menus, and windows used to create an automaton, one should first read the tutorial on finite automata. For knowledge of regular expressions and how JFLAP defines and implements them, one should first read the tutorial on regular expressions.

Pumping lemma for regularlanguages
In the theory of formal languages, the pumping lemma for regular languages describes an essential property of all regular languages. Informally, it says that all sufficiently long words in a regular language may be pumped — that is, have a middle section of the word repeated an arbitrary number of times — to produce a new word that also lies within the same language.
Specifically, the pumping lemma says that for any regular language L there exists a constant p such that any word w in L with length at least p can be split into three substrings, w = xyz, where the middle portion y must not be empty, such that the words xz, xyz, xyyz, xyyyz, … constructed by repeating y an arbitrary number of times (including zero times) are still in L. This process of repetition is known as "pumping". Moreover, the pumping lemma guarantees that the length of xy will be at most p, imposing a limit on the ways in which w may be split. Finite languages trivially satisfy the pumping lemma by having p equal to the maximum string length in L plus one.
The pumping lemma was first proved by Dana Scott and Michael Rabin in 1959. It was rediscovered shortly after by Yehoshua Bar-Hillel, Micha A. Perles, and Eli Shamir in 1961. It is useful for disproving the regularity of a specific language in question. It is one of a few pumping lemmas, each with a similar purpose.
Use of lemma
The pumping lemma is often used to prove that a particular language is non-regular: a proof by contradiction (of the languages regularity) may consist of exhibiting a word (of the required length) in the language which lacks the property outlined in the pumping lemma.
For example the language L = {anbn : n ? 0} over the alphabet ? = {a, b} can be shown to be non-regular as follows. Let w, x, y, z, p, and i be as used in the formal statement for the pumping lemma above. Let w in L be given by w = apbp. By the pumping lemma, there must be some decomposition w = xyz with |xy| ? p and |y| ? 1 such that xyiz in L for every i ? 0. Using |xy| ? p, we know y only consists of instances of a. Moreover, because |y| ? 1, it contains at least one instance of the letter a. We now pump y up: xy2z has more instances of the letter a than the letter b, since we have added some instances of a without adding instances of b. Therefore xy2z is not in L. We have reached a contradiction. Therefore, the assumption that L is regular must be incorrect. Hence L is not regular.
The proof that the language of balanced (i.e., properly nested) parentheses is not regular follows the same idea. Given p, there is a string of balanced parentheses that begins with more than p left parentheses, so that y will consist entirely of left parentheses. By repeating y, we can produce a string that does not contain the same number of left and right parentheses, and so they cannot be balanced.
Context Free Grammars and Languages
In formal language theory, a context-free grammar (CFG) is a formal grammar in which every production rule is of the form
where V is a single nonterminal symbol, and w is a string of terminals and/or nonterminals (w can be empty). A formal grammar is considered "context free" when its production rules can be applied regardless of the context of a nonterminal. No matter which symbols surround it, the single nonterminal on the left hand side can always be replaced by the right hand side.
Languages generated by context-free grammars are known as context-free languages (CFL). Different context-free grammars can generate the same context-free language. It is important to distinguish properties of the language (intrinsic properties) from properties of a particular grammar (extrinsic properties). Given two context-free grammars, the language equality question (do they generate the same language?) is undecidable.
Context-free grammars are important in linguistics for describing the structure of sentences and words in natural language, and in computer science for describing the structure of programming languages and other formal languages.
In linguistics, some authors use the term phrase structure grammar to refer to context-free grammars, whereby phrase structure grammars are distinct from dependency grammars. In computer science, a popular notation for context-free grammars is Backus–Naur Form, or BNF.
A context-free grammar G is defined by the 4-tupple
 where
where
 is a finite set; each element
is a finite set; each element  is called a non-terminal character or a variable.
Each variable represents a different type of phrase or clause in the
sentence. Variables are also sometimes called syntactic categories. Each
variable defines a sub-language of the language defined by
is called a non-terminal character or a variable.
Each variable represents a different type of phrase or clause in the
sentence. Variables are also sometimes called syntactic categories. Each
variable defines a sub-language of the language defined by  .
.2.
 is a finite set of terminals, disjoint from
is a finite set of terminals, disjoint from  , which make up the actual content of the sentence. The set of terminals is the alphabet of the language defined by the grammar
, which make up the actual content of the sentence. The set of terminals is the alphabet of the language defined by the grammar  .
.3.
 is a finite relation from
is a finite relation from  to
to  , where the asterisk represents the Kleene star operation. The members of
, where the asterisk represents the Kleene star operation. The members of  are called the (rewrite) rules or productions of the grammar. (also commonly symbolized by a
are called the (rewrite) rules or productions of the grammar. (also commonly symbolized by a  )
)4.
 is the start variable (or start symbol), used to represent the whole sentence (or program). It must be an element of
is the start variable (or start symbol), used to represent the whole sentence (or program). It must be an element of  .
.Leftmost, Rightmost derivations
Now consider the grammar
G = ({S, A, B, C}, {a, b, c}, S, P)
where
P = {S![]() ABC, A
ABC, A![]() aA,
A
aA,
A![]()
![]() ,
B
,
B![]() bB, B
bB, B![]()
![]() ,
C
,
C![]() cC, C
cC, C![]()
![]() }.
}.
With this grammar, there is a choice of variables to expand. Here is a sample derivation:
S ![]() ABC
ABC ![]() aABC
aABC ![]() aABcC
aABcC ![]() aBcC
aBcC ![]() abBcC
abBcC ![]() abBc
abBc ![]() abbBc
abbBc ![]() abbc
abbc
If we always expanded the leftmost variable first, we would have a leftmost derivation:
S ![]() ABC
ABC ![]() aABC
aABC ![]() aBC
aBC ![]() abBC
abBC ![]() abbBC
abbBC ![]() abbC
abbC ![]() abbcC
abbcC ![]() abbc
abbc
Conversely, if we always expanded the rightmost variable first, we would have a rightmost derivation:
S ![]() ABC
ABC ![]() ABcC
ABcC ![]() ABc
ABc ![]() AbBc
AbBc ![]() AbbBc
AbbBc ![]() Abbc
Abbc ![]() aAbbc
aAbbc ![]() abbc
abbc
There are two things to notice here:
1. Different derivations result in quite different sentential forms, but
2. For a context-free grammar,
it really doesnt make much difference in what order we expand
the variables.
Chomsky normal form (CNF)
In formal language theory, a context-free grammar is said to be in Chomsky normal form (named for Noam Chomsky) if all of its production rules are of the form: or
or or
or ,
,
 ,
,  and
and  are nonterminal symbols,
are nonterminal symbols,  is a terminal symbol (a symbol that represents a constant value),
is a terminal symbol (a symbol that represents a constant value),  is the start symbol, and
is the start symbol, and  is the empty string. Also, neither
is the empty string. Also, neither  nor
nor  may be the start symbol, and the third production rule can only appear if
may be the start symbol, and the third production rule can only appear if  is in
is in  , namely, the language produced by the context-free grammar
, namely, the language produced by the context-free grammar  .
.
Every grammar in Chomsky normal form is context free,
and conversely, every context-free grammar can be transformed into an
equivalent one which is in Chomsky normal form. Several algorithms for
performing such a transformation are known. Transformations are
described in most textbooks on automata theory, such as Hopcroft and
Ullman, 1979.[1] As pointed out by Lange and Leiß,[2]
the drawback of these transformations is that they can lead to an
undesirable bloat in grammar size. The size of a grammar is the sum of
the sizes of its production rules, where the size of a rule is one plus
the length of its right-hand side. Using  to denote the size of the original grammar
to denote the size of the original grammar  , the size blow-up in the worst case may range from
, the size blow-up in the worst case may range from  to
to  , depending on the transformation algorithm used.
, depending on the transformation algorithm used.
In computer science and formal language theory, a context-free grammar is in Greibach normal form (GNF) if the right-hand sides of all production rules start with a terminal symbol, optionally followed by some variables. A non-strict form allows one exception to this format restriction for allowing the empty word (epsilon, ?) to be a member of the described language. The normal form was established by Sheila Greibach and it bears her name.
More precisely, a context-free grammar is in Greibach normal form, if all production rules are of the form:
where
 is a nonterminal symbol,
is a nonterminal symbol,  is a terminal symbol,
is a terminal symbol,  is a (possibly empty) sequence of nonterminal symbols not including the start symbol, S is the start symbol, and ? is the empty word.
is a (possibly empty) sequence of nonterminal symbols not including the start symbol, S is the start symbol, and ? is the empty word.Observe that the grammar does not have left recuesions.
Every context-free grammar can be transformed into an equivalent grammar in Greibach normal form.[1]
Various constructions exist. Some do not permit the second form of rule
and cannot transform context-free grammars that can generate the empty
word. For one such construction the size of the constructed grammar is O(n4) in the general case and O(n3) if no derivation of the original grammar consists of a single nonterminal symbol, where n is the size of the original grammar. This conversion can be used to prove that every context free language can be accepted by a non-deterministic pushdown automaton. Given a grammar in GNF and a derivable string in the grammar with length n, any top-down parser will halt at depth n.
pushdown automaton

In computer science, a pushdown automaton (PDA) is a type of automaton that employs a stack.
Pushdown automata are used in theories about what can be computed by machines. They are more capable than finite-state machines but less capable than Turing machines. Deterministic pushdown automata can recognize all deterministic context-free languages while nondeterministic ones can recognize all context-free languages. Mainly the former are used in parser design.
The term "pushdown" refers to the fact that the stack can be regarded as being "pushed down" like a tray dispenser at a cafeteria, since the operations never work on elements other than the top element. A stack automaton, by contrast, does allow access to and operations on deeper elements. Stack automata can recognize a strictly larger set of languages than pushdown automata.[1] A nested stack automaton allows full access, and also allows stacked values to be entire sub-stacks rather than just single finite symbols.
Pushdown automata differ from finite state machines in two ways:
1. They can use the top of the stack to decide which transition to take.
2. They can manipulate the stack as part of performing a transition.
Pushdown automata choose a transition by indexing a table by input signal, current state, and the symbol at the top of the stack. This means that those three parameters completely determine the transition path that is chosen. Finite state machines just look at the input signal and the current state: they have no stack to work with. Pushdown automata add the stack as a parameter for choice.
Pushdown automata can also manipulate the stack, as part of performing a transition. Finite state machines choose a new state, the result of following the transition. The manipulation can be to push a particular symbol to the top of the stack, or to pop off the top of the stack. The automaton can alternatively ignore the stack, and leave it as it is. The choice of manipulation (or no manipulation) is determined by the transition table.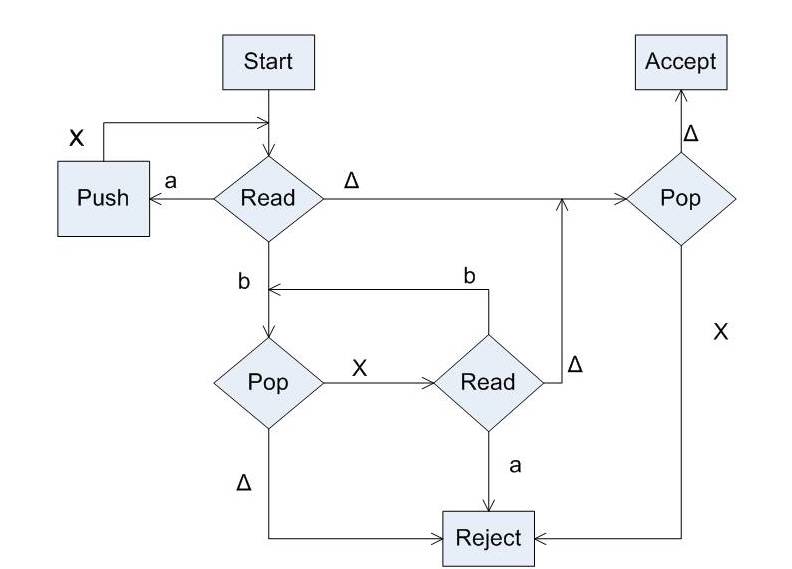
Put together: Given an input signal, current state, and stack symbol, the automaton can follow a transition to another state, and optionally manipulate (push or pop) the stack.
In general, pushdown automata may have several computations on a given input string, some of which may be halting in accepting configurations. If only one computation exists for all accepted strings, the result is a deterministic pushdown automaton (DPDA) and the language of these strings is a deterministic context-free language. Not all context-free languages are deterministic. As a consequence of the above the DPDA is a strictly weaker variant of the PDA and there exists no algorithm for converting a PDA to an equivalent DPDA, if such a DPDA exists.
If we allow a finite automaton access to two stacks instead of just one, we obtain a more powerful device, equivalent in power to a Turing machine. A linear bounded automaton is a device which is more powerful than a pushdown automaton but less so than a Turing machine.
We use standard formal language notation:  denotes the set of strings over alphabet
denotes the set of strings over alphabet  and
and  denotes the empty string.
denotes the empty string.
A PDA is formally defined as a 7-tuple:
 where
where
 is a finite set of states
is a finite set of states Sigma is a finite set which is called the input alphabet
Sigma is a finite set which is called the input alphabet Gamma is a finite set which is called the stack alphabet
Gamma is a finite set which is called the stack alphabet delta is a finite subset of ,
delta is a finite subset of ,  the transition relation.
the transition relation. is the start state
is the start state Gamma is the initial stack symbol
Gamma is the initial stack symbol is the set of accepting states
is the set of accepting states
An element  is a transition of
is a transition of  . It has the intended meaning that
. It has the intended meaning that  , in state
, in state  , with
, with  on the input and with
on the input and with  as topmost stack symbol, may read
as topmost stack symbol, may read  , change the state to
, change the state to  , pop
, pop  , replacing it by pushing
, replacing it by pushing  . The
. The  component of the transition relation is used to formalize that the PDA
can either read a letter from the input, or proceed leaving the input
untouched.
component of the transition relation is used to formalize that the PDA
can either read a letter from the input, or proceed leaving the input
untouched.
In many texts the transition relation is replaced by an (equivalent) formalization, where
 is the transition function, mapping
is the transition function, mapping  into finite subsets of
into finite subsets of 
Here
 contains all possible actions in state
contains all possible actions in state  with
with  on the stack, while reading
on the stack, while reading  on the input. One writes
on the input. One writes  forhttp://www.alchetron.com/redsigma/dataComponentWelcomePageRouterServlet?displayName=Automata_Theory&module=T&id=883&userId=faeb44ab69b2c3fcb8535dfbe9dfb8a8&accordionTabId=1&fromSearch=N&visibility=WORLD the function precisely when
forhttp://www.alchetron.com/redsigma/dataComponentWelcomePageRouterServlet?displayName=Automata_Theory&module=T&id=883&userId=faeb44ab69b2c3fcb8535dfbe9dfb8a8&accordionTabId=1&fromSearch=N&visibility=WORLD the function precisely when  for the relation.
for the relation.PDA and Context-free Languages
Every context-free grammar can be transformed into an equivalent nondeterministic pushdown automaton. The derivation process of the grammar is simulated in a leftmost way. Where the grammar rewrites a nonterminal, the PDA takes the topmost nonterminal from its stack and replaces it by the right-hand part of a grammatical rule (expand). Where the grammar generates a terminal symbol, the PDA reads a symbol from input when it is the topmost symbol on the stack (match). In a sense the stack of the PDA contains the unprocessed data of the grammar, corresponding to a pre-order traversal of a derivation tree.
Technically, given a context-free grammar, the PDA is constructed as follows.
 for each rule
for each rule  (expand)
(expand) for each terminal symbol
for each terminal symbol  (match)
(match)As a result we obtain a single state pushdown automata, the state here is
 , accepting the context-free language by empty stack. Its initial stack symbol equals the axiom of the context-free grammar.
, accepting the context-free language by empty stack. Its initial stack symbol equals the axiom of the context-free grammar.
The converse, finding a grammar for a given PDA, is not that easy. The trick is to code two states of the PDA into the nonterminals of the grammar.
Theorem. For each pushdown automaton  one may construct a context-free grammar
one may construct a context-free grammar  such that
such that  .
.
A Turing machine is a hypothetical device that manipulates symbols on a strip of tape according to a table of rules. Despite its simplicity, a Turing machine can be adapted to simulate the logic of any computer algorithm, and is particularly useful in explaining the functions of a CPU inside a computer.
The "Turing" machine was invented in 1936 by Alan Turing who called it an "a-machine" (automatic machine). The Turing machine is not intended as practical computing technology, but rather as a hypothetical device representing a computing machine. Turing machines help computer scientists understand the limits of mechanical computation.
Turing gave a succinct definition of the experiment in his 1948 essay, "Intelligent Machinery". Referring to his 1936 publication, Turing wrote that the Turing machine, here called a Logical Computing Machine, consisted of:
...an unlimited memory capacity obtained in the form of an infinite tape marked out into squares, on each of which a symbol could be printed. At any moment there is one symbol in the machine; it is called the scanned symbol. The machine can alter the scanned symbol and its behavior is in part determined by that symbol, but the symbols on the tape elsewhere do not affect the behavior of the machine. However, the tape can be moved back and forth through the machine, this being one of the elementary operations of the machine. Any symbol on the tape may therefore eventually have an innings. (Turing 1948, p. 3)
A Turing machine that is able to simulate any other Turing machine is called a universal Turing machine (UTM, or simply a universal machine). A more mathematically-oriented definition with a similar "universal" nature was introduced by Alonzo Church, whose work on lambda calculus intertwined with Turings in a formal theory of computation known as the Church–Turing thesis. The thesis states that Turing machines indeed capture the informal notion of effective methods in logic and mathematics, and provide a precise definition of an algorithm or "mechanical procedure". Studying their abstract properties yields many insights into computer science and complexity theory.

The Turing machine mathematically models a machine that mechanically operates on a tape. On this tape are symbols, which the machine can read and write, one at a time, using a tape head. Operation is fully determined by a finite set of elementary instructions such as "in state 42, if the symbol seen is 0, write a 1; if the symbol seen is 1, change into state 17; in state 17, if the symbol seen is 0, write a 1 and change to state 6;" etc. In the original article ("On computable numbers, with an application to the Entscheidungsproblem", see also references below), Turing imagines not a mechanism, but a person whom he calls the "computer", who executes these deterministic mechanical rules slavishly (or as Turing puts it, "in a desultory manner").
The head is always over a particular square of the tape; only a finite stretch of squares is shown. The instruction to be performed (q4) is shown over the scanned square. (Drawing after Kleene (1952) p.375.)
Recursively enumerable languages
In mathematics, logic and computer science, a formal language is called recursively enumerable (also recognizable, partially decidable, semidecidable or Turing-acceptable) if it is a recursively enumerable subset in the set of all possible words over the alphabet of the language, i.e., if there exists a Turing machine which will enumerate all valid strings of the language.
Recursively enumerable languages are known as type-0 languages in the Chomsky hierarchy of formal languages. All regular, context-free, context-sensitive and recursive languages are recursively enumerable.
The class of all recursively enumerable languages is called RE.
unsolvable problems:Halting Problem
In computability theory, the halting problem can be stated as follows: "Given a description of an arbitrary computer program, decide whether the program finishes running or continues to run forever". This is equivalent to the problem of deciding, given a program and an input, whether the program will eventually halt when run with that input, or will run forever.
Alan Turing proved in 1936 that a general algorithm to solve the halting problem for all possible program-input pairs cannot exist. A key part of the proof was a mathematical definition of a computer and program, which became known as a Turing machine; the halting problem is undecidable over Turing machines. It is one of the first examples of a decision problem.
Jack Copeland (2004) attributes the term halting problem to Martin Davis.
The halting problem is a decision problem about properties of computer programs on a fixed Turing-complete model of computation, i.e. all programs that can be written in some given programming language that is general enough to be equivalent to a Turing machine. The problem is to determine, given a program and an input to the program, whether the program will eventually halt when run with that input. In this abstract framework, there are no resource limitations on the amount of memory or time required for the programs execution; it can take arbitrarily long, and use arbitrarily much storage space, before halting. The question is simply whether the given program will ever halt on a particular input.

The halting problem is historically important because it was one of the first problems to be proved undecidable. (Turings proof went to press in May 1936, whereas Alonzo Churchs proof of the undecidability of a problem in the lambda calculus had already been published in April 1936.) Subsequently, many other undecidable problems have been described; the typical method of proving a problem to be undecidable is with the technique of reduction. To do this, it is sufficient to show that if a solution to the new problem were found, it could be used to decide an undecidable problem by transforming instances of the undecidable problem into instances of the new problem. Since we already know that no method can decide the old problem, no method can decide the new problem either. Often the new problem is reduced to solving the halting problem.
