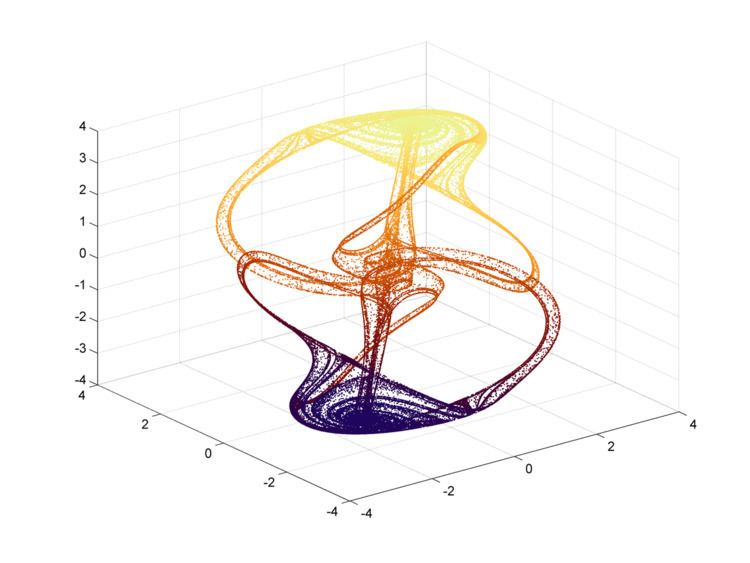
In the dynamical systems theory, Thomas' cyclically symmetric attractor is a 3D strange attractor originally proposed by René Thomas. It has a simple form which is cyclically symmetric in the x,y, and z variables and can be viewed as the trajectory of a frictionally dampened particle moving in a 3D lattice of forces. The simple form has made it a popular example.
It is described by the differential equations
d x d t = sin ( y ) − b x d y d t = sin ( z ) − b y d z d t = sin ( x ) − b z where b is a constant.
b corresponds to how dissipative the system is, and acts as a bifurcation parameter. For b > 1 the origin is the single stable equilibrium. At b = 1 it undergoes a pitchfork bifurcation, splitting into two attractive fixed points. As the parameter is decreased further they undergo a Hopf bifurcation at b ≈ 0.32899 , creating a stable limit cycle. The limit cycle the undergoes a period doubling cascade and becomes chaotic at b ≈ 0.208186 . Beyond this the attractor expands, undergoing a series of crises (up to six separate attractors can coexist for certain values). The fractal dimension of the attractor increases towards 3.
In the limit b = 0 the system lacks dissipation and the trajectory ergodically wanders the entire space (with an exception for 1.67%, where it drifts parallel to one of the coordinate axes: this corresponds to quasiperiodic torii). The dynamics has been described as deterministic fractional Brownian motion, and exhibits anomalous diffusion.