Girish Mahajan (Editor)

Thévenin's theorem

Updated on
Edit
Like
Comment
Share on FacebookTweet on TwitterShare on LinkedInShare on Reddit
Thévenin's theorem

As originally stated in terms of DC resistive circuits only, Thévenin's theorem holds that:

Contents

  • Any linear electrical network with voltage and current sources and only resistances can be replaced at terminals A-B by an equivalent voltage source Vth in series connection with an equivalent resistance Rth.
  • The equivalent voltage Vth is the voltage obtained at terminals A-B of the network with terminals A-B open circuited.
  • The equivalent resistance Rth is the resistance that the circuit between terminals A and B would have if all ideal voltage sources in the circuit were replaced by a short circuit and all ideal current sources were replaced by an open circuit.
  • If terminals A and B are connected to one another, the current flowing from A to B will be Vth/Rth. This means that Rth could alternatively be calculated as Vth divided by the short-circuit current between A and B when they are connected together.

    • In circuit theory terms, the theorem allows any one-port network to be reduced to a single voltage source and a single impedance.

    The theorem also applies to frequency domain AC circuits consisting of reactive and resistive impedances. It means the theorem applies for AC in an exactly same way to DC except that resistances are generalized to impedances.

    The theorem was independently derived in 1853 by the German scientist Hermann von Helmholtz and in 1883 by Léon Charles Thévenin (1857–1926), an electrical engineer with France's national Postes et Télégraphes telecommunications organization.

    Thévenin's theorem and its dual, Norton's theorem, are widely used to make circuit analysis simpler and to study a circuit's initial-condition and steady-state response. Thévenin's theorem can be used to convert any circuit's sources and impedances to a Thévenin equivalent; use of the theorem may in some cases be more convenient than use of Kirchhoff's circuit laws.

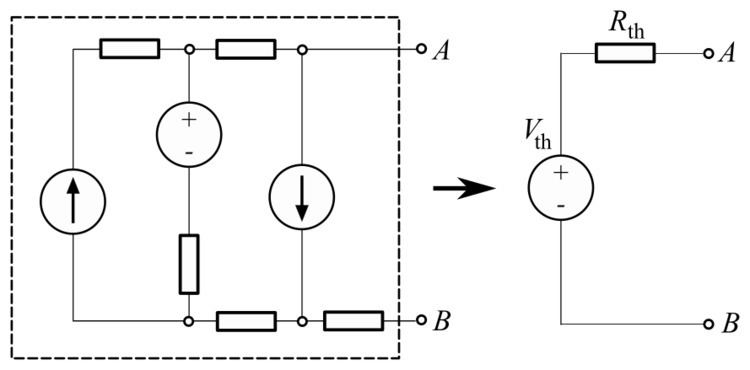
    Calculating the Thévenin equivalent

    The equivalent circuit is a voltage source with voltage VTh in series with a resistance RTh.

    The Thévenin-equivalent voltage VTh is the voltage at the output terminals of the original circuit.It is the open circuited voltage at the output terminals of the original circuit. When calculating a Thévenin-equivalent voltage, the voltage divider principle is often useful, by declaring one terminal to be Vout and the other terminal to be at the ground point.

    The Thévenin-equivalent resistance RTh is the resistance measured across points A and B "looking back" into the circuit. It is important to first replace all voltage- and current-sources with their internal resistances. For an ideal voltage source, this means replace the voltage source with a short circuit. For an ideal current source, this means replace the current source with an open circuit. Resistance can then be calculated across the terminals using the formulae for series and parallel circuits. This method is valid only for circuits with independent sources. If there are dependent sources in the circuit, another method must be used such as connecting a test source across A and B and calculating the voltage across or current through the test source.

    Note that the replacement of voltage and current sources do the opposite of what the sources themselves are meant to do. A voltage source creates a difference of electric potential between its terminals; its replacement in Thévenin's theorem resistance calculations, a short circuit, equalizes potential. Likewise, a current source's aim is to generate a certain amount of current, whereas an open circuit stops electric flow altogether.

    Example

    In the example, calculating the equivalent voltage:

    V T h = R 2 + R 3 ( R 2 + R 3 ) + R 4 ⋅ V 1 = 1 k Ω + 1 k Ω ( 1 k Ω + 1 k Ω ) + 2 k Ω ⋅ 15 V = 1 2 ⋅ 15 V = 7.5 V

    (notice that R1 is not taken into consideration, as above calculations are done in an open circuit condition between A and B, therefore no current flows through this part, which means there is no current through R1 and therefore no voltage drop along this part)

    Calculating equivalent resistance:

    R T h = R 1 + [ ( R 2 + R 3 ) ∥ R 4 ] = 1 k Ω + [ ( 1 k Ω + 1 k Ω ) ∥ 2 k Ω ] = 1 k Ω + ( 1 ( 1 k Ω + 1 k Ω ) + 1 ( 2 k Ω ) ) − 1 = 2 k Ω .

    Conversion to a Norton equivalent

    A Norton equivalent circuit is related to the Thévenin equivalent by

    R T h = R N o V T h = I N o R N o I N o = V T h / R T h .

    Practical limitations

  • Many circuits are only linear over a certain range of values, thus the Thévenin equivalent is valid only within this linear range.
  • The Thévenin equivalent has an equivalent I–V characteristic only from the point of view of the load.
  • The power dissipation of the Thévenin equivalent is not necessarily identical to the power dissipation of the real system. However, the power dissipated by an external resistor between the two output terminals is the same regardless of how the internal circuit is implemented.

    • A proof of the theorem

    The proof involves two steps. First use superposition theorem to construct a solution. Then, use uniqueness theorem to show the solution is unique. The second step is usually implied. First, using the superposition theorem, in general for any linear "black box" circuit which contains voltage sources and resistors, one can always write down its voltage as a linear function of the corresponding current as follows

    V = V E q − Z E q I

    where the first term reflects the linear summation of contributions from each voltage source, while the second term measures the contribution from all the resistors. The above argument is due to the fact that the voltage of the black box for a given current I is identical to the linear superposition of the solutions of the following problems: (1) to leave the black box open circuited but activate individual voltage source one at a time and, (2) to short circuit all the voltage sources but feed the circuit with a certain ideal voltage source so that the resulting current exactly reads I (or an ideal current source of current I ). Once the above expression is established, it is straightforward to show that V E q and Z E q are the single voltage source and the single series resistor in question.

    References

    Thévenin's theorem Wikipedia
    (Text) CC BY-SA


    Similar Topics