In theoretical computer science, stuttering equivalence, a relation written as
π ∼ s t π ′ ,
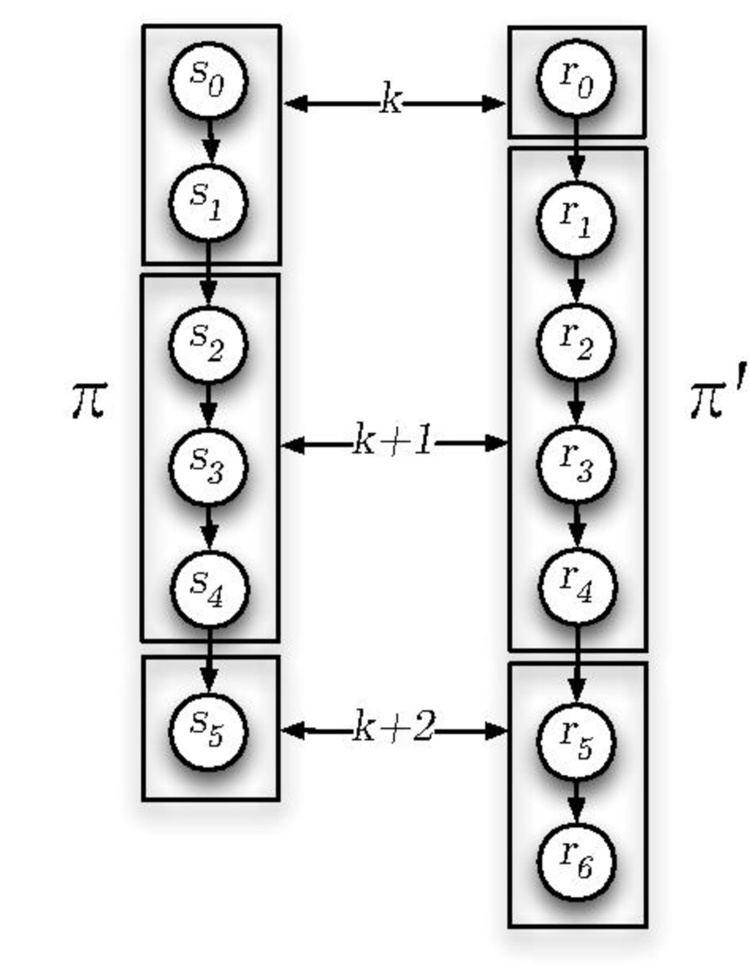
can be seen as a partitioning of path π and π ′ into blocks, so that states in the k t h block of one path are labeled ( L ( ⋅ ) ) the same as states in the k t h block of the other path. Corresponding blocks may have different lengths.
Formally, this can be expressed as two infinite paths π = s 0 , s 1 , … and π ′ = r 0 , r 1 , … which are stuttering equivalent ( π ∼ s t π ′ ) if there are two infinite sequences of integers 0 = i 0 < i 1 < i 2 < … and 0 = j 0 < j 1 < j 2 < … such that for every block k ≥ 0 holds L ( s i k ) = L ( s i k + 1 ) = … = L ( s i k + 1 − 1 ) = L ( r j k ) = L ( r j k + 1 ) = … = L ( r j k + 1 − 1 ) .
Stuttering equivalence is not the same as bisimulation, since bisimulation cannot capture the semantics of the 'eventually' (or 'finally') operator found in linear temporal/computation tree logic(branching time logic)(modal logic). So-called branching bisimulation has to be used.