Parameters none Median 0 | Mean Does not exist | |
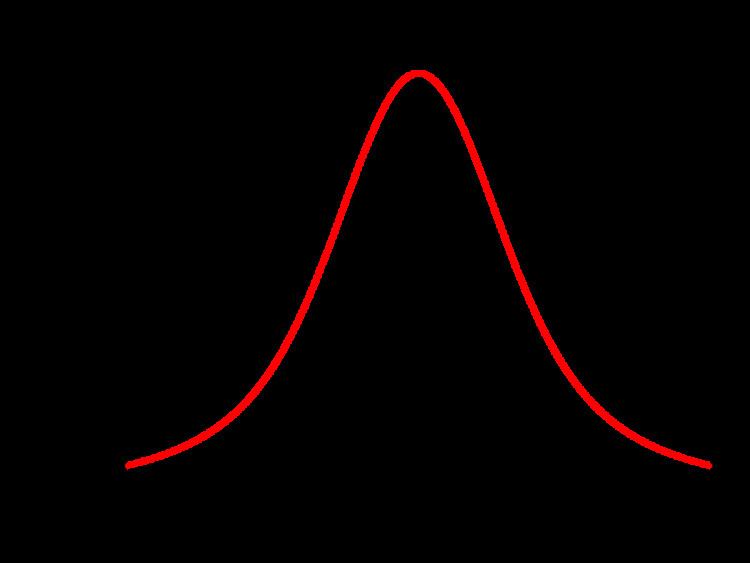 | ||
Support x ∈ ( − ∞ , ∞ ) {\displaystyle x\in (-\infty ,\infty )} PDF φ ( 0 ) − φ ( x ) x 2 {\displaystyle {\frac {\varphi (0)-\varphi (x)}{x^{2}}}} CDF { Φ ( x ) − [ φ ( 0 ) − φ ( x ) ] / x x ≠ 0 1 / 2 x = 0 {\displaystyle {\begin{cases}\Phi (x)-\left[\varphi (0)-\varphi (x)\right]/x&x\neq 0\\1/2&x=0\\\end{cases}}} | ||
In probability theory, the slash distribution is the probability distribution of a standard normal variate divided by an independent standard uniform variate. In other words, if the random variable Z has a normal distribution with zero mean and unit variance, the random variable U has a uniform distribution on [0,1] and Z and U are statistically independent, then the random variable X = Z / U has a slash distribution. The slash distribution is an example of a ratio distribution. The distribution was named by William H. Rogers and John Tukey in a paper published in 1972.
The probability density function (pdf) is
where φ(x) is the probability density function of the standard normal distribution. The result is undefined at x = 0, but the discontinuity is removable:
The most common use of the slash distribution is in simulation studies. It is a useful distribution in this context because it has heavier tails than a normal distribution, but it is not as pathological as the Cauchy distribution.
Differential equation
The pdf of the slash distribution is a solution of the following differential equation:
