 | ||
In mathematical analysis, the rising sun lemma is a lemma due to Frigyes Riesz, used in the proof of the Hardy–Littlewood maximal theorem. The lemma was a precursor in one dimension of the Calderón–Zygmund lemma.
The lemma is stated as follows:
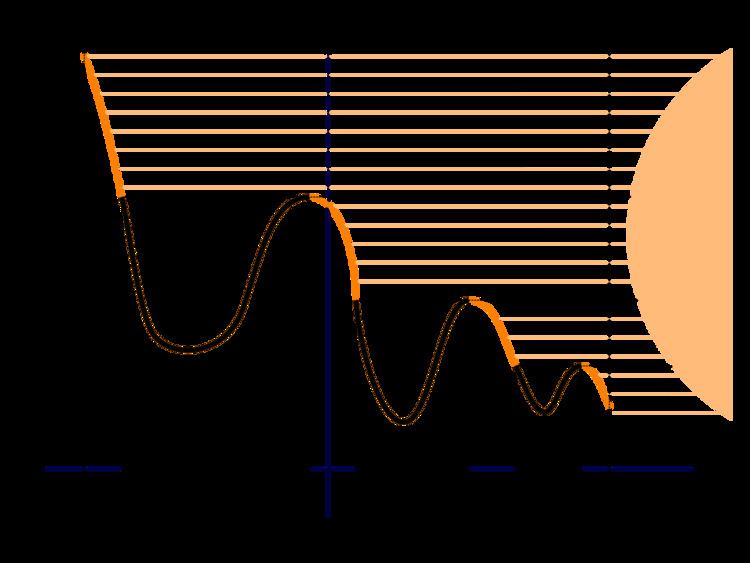
Suppose g is a real-valued continuous function on the interval [a,b] and S is the set of x in [a,b] such that g(x) < g(y) for some y with x < y ≤ b. (Note that b is not in S, though a may be.) Define E = S ∩ (a,b).Then E is an open set, and it may be written as a countable union of disjoint intervalsThe colorful name of the lemma comes from imagining the graph of the function g as a mountainous landscape, with the sun shining horizontally from the right. The set E consist of points that are in the shadow.
Proof
We need a lemma: Suppose [c,d) ⊂ S, but d ∉ S. Then g(c) < g(d). To prove this, suppose g(c) ≥ g(d). Then g achieves its maximum on [c,d] at some point z < d. Since z ∈ S, there is a y in (z,b] with g(z) < g(y). If y ≤ d, then g would not reach its maximum on [c,d] at z. Thus, y ∈ (d,b], and g(d) ≤ g(z) < g(y). This means that d ∈ S, which is a contradiction, thus establishing the lemma.
The set E is open, so it is composed of a countable union of disjoint intervals (ak,bk).
It follows immediately from the lemma that g(x) < g(bk) for x in (ak,bk). Since g is continuous, we must also have g(ak) ≤ g(bk).
If ak ≠ a or a ∉ S, then ak ∉ S, so g(ak) ≥ g(bk), for otherwise ak ∈ S. Thus, g(ak) = g(bk) in these cases.
Finally, if ak = a ∈ S, the lemma tells us that g(a) < g(bk).
