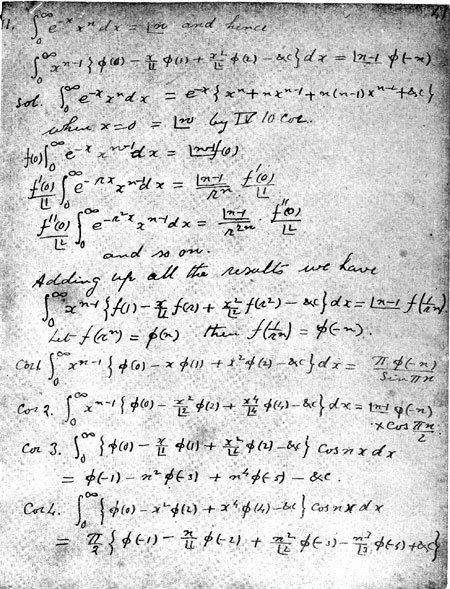Suvarna Garge (Editor)

Ramanujan's master theorem

Updated on
Edit
Like
Comment
Share on FacebookTweet on TwitterShare on LinkedInShare on Reddit
Ramanujan's master theorem

In mathematics, Ramanujan's master theorem (named after mathematician Srinivasa Ramanujan) is a technique that provides an analytic expression for the Mellin transform of an analytic function.

Contents

The result is stated as follows:

If a complex-valued function f ( x ) has an expansion of the form

f ( x ) = ∑ k = 0 ∞ ϕ ( k ) k ! ( − x ) k

then the Mellin transform of f ( x ) is given by

∫ 0 ∞ x s − 1 f ( x ) d x = Γ ( s ) ϕ ( − s )

where Γ ( s ) is the gamma function.

It was widely used by Ramanujan to calculate definite integrals and infinite series.

Higher-dimensional versions of this theorem also appear in quantum physics (through Feynman diagrams).

A similar result was also obtained by J. W. L. Glaisher.

Alternative formalism

An alternative formulation of Ramanujan's master theorem is as follows:

∫ 0 ∞ x s − 1 ( λ ( 0 ) − x λ ( 1 ) + x 2 λ ( 2 ) − ⋯ ) d x = π sin ⁡ ( π s ) λ ( − s )

which gets converted to the above form after substituting λ ( n ) = ϕ ( n ) Γ ( 1 + n ) and using the functional equation for the gamma function.

The integral above is convergent for 0 < Re ⁡ ( s ) < 1 .

Proof

The proof of Ramanujan's Master Theorem provided by G. H. Hardy employs the Cauchy's residue theorem and the well-known Mellin inversion theorem.

Application to Bernoulli polynomials

The generating function of the Bernoulli polynomials B k ( x ) is given by:

z e x z e z − 1 = ∑ k = 0 ∞ B k ( x ) z k k !

These polynomials are given in terms of Hurwitz zeta function:

ζ ( s , a ) = ∑ n = 0 ∞ 1 ( n + a ) s

by ζ ( 1 − n , a ) = − B n ( a ) n for n ≥ 1 . By means of Ramanujan master theorem and generating function of Bernoulli polynomials one will have following integral representation:

∫ 0 ∞ x s − 1 ( e − a x 1 − e − x − 1 x ) d x = Γ ( s ) ζ ( s , a )

valid for 0 < Re ⁡ ( s ) < 1 .

Application to the Gamma function

Weierstrass's definition of the Gamma function

Γ ( x ) = e − γ x x ∏ n = 1 ∞ ( 1 + x n ) − 1 e x / n

is equivalent to expression

log ⁡ Γ ( 1 + x ) = − γ x + ∑ k = 2 ∞ ζ ( k ) k ( − x ) k

where ζ ( k ) is the Riemann zeta function.

Then applying Ramanujan master theorem we have:

∫ 0 ∞ x s − 1 γ x + log ⁡ Γ ( 1 + x ) x 2 d x = π sin ⁡ ( π s ) ζ ( 2 − s ) 2 − s

valid for 0 < R e ( s ) < 1 .

Special cases of s = 1 2 and s = 3 4 are

∫ 0 ∞ γ x + log ⁡ Γ ( 1 + x ) x 5 / 2 d x = 2 π 3 ζ ( 3 2 ) ∫ 0 ∞ γ x + log ⁡ Γ ( 1 + x ) x 9 / 4 d x = 2 4 π 5 ζ ( 5 4 )

Mathematica 7 is unable to compute these examples.

References

Ramanujan's master theorem Wikipedia
(Text) CC BY-SA