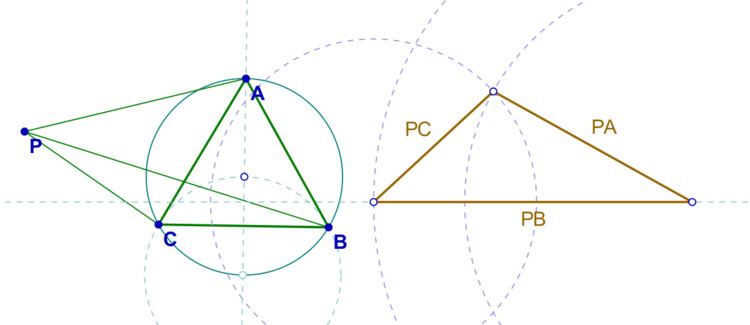
Pompeiu's theorem

Pompeiu's theorem is a result of plane geometry, discovered by the Romanian mathematician Dimitrie Pompeiu. The theorem is quite simple, but not classical. It states the following:

The proof is quick. Consider a rotation of 60° about the point C. Assume A maps to B, and P maps to P '. Then we have P C   =   P ′ C , and ∠ P C P ′   =   60 ∘ . Hence triangle PCP ' is equilateral and P P ′   =   P C . It is obvious that P A   =   P ′ B . Thus, triangle PBP ' has sides equal to PA, PB, and PC and the proof by construction is complete.

Further investigations reveal that if P is not in the interior of the triangle, but rather on the circumcircle, then PA, PB, PC form a degenerate triangle, with the largest being equal to the sum of the others.