 | ||
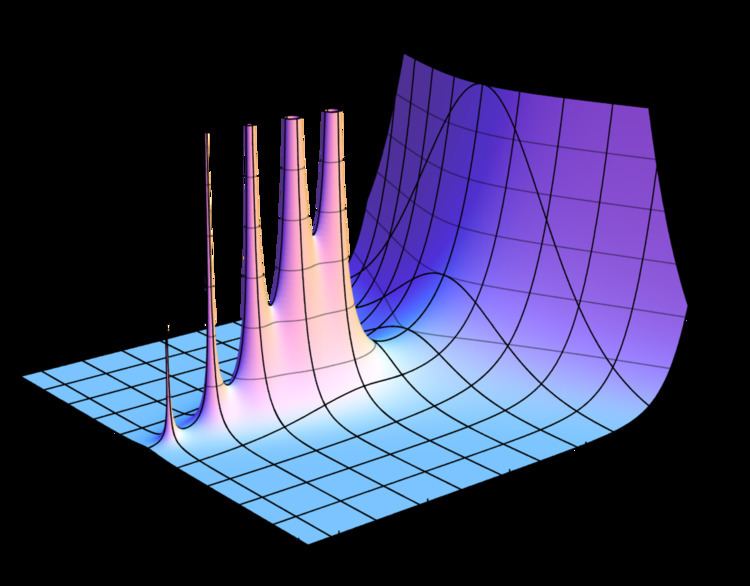
In the mathematical field of complex analysis, a pole of a meromorphic function is a certain type of singularity that behaves like the singularity of
Contents
Definition
Formally, suppose U is an open subset of the complex plane C, p is an element of U and f : U \ {p} → C is a function which is holomorphic over its domain. If there exists a holomorphic function g : U → C, such that g(p) is nonzero, and a positive integer n, such that for all z in U \ {p}
holds, then p is called a pole of f. The smallest such n is called the order of the pole. A pole of order 1 is called a simple pole.
A few authors allow the order of a pole to be zero, in which case a pole of order zero is either a regular point or a removable singularity. However, it is more usual to require the order of a pole to be positive.
From above several equivalent characterizations can be deduced:
If n is the order of pole p, then necessarily g(p) ≠ 0 for the function g in the above expression. So we can put
for some h that is holomorphic in an open neighborhood of p and has a zero of order n at p. So informally one might say that poles occur as reciprocals of zeros of holomorphic functions.
Also, by the holomorphy of g, f can be expressed as:
This is a Laurent series with finite principal part. The holomorphic function
Pole at infinity
A complex function can be defined as having a pole at the point at infinity. In this case U has to be a neighborhood of infinity, such as the exterior of any closed ball. To use the previous definition, a meaning for g being holomorphic at ∞ is needed. Alternately, a definition can be given starting from the definition at a finite point by suitably mapping the point at infinity to a finite point. The map
Pole of a function on a complex manifold
In general, having a function
Examples
Terminology and generalizations
If the first derivative of a function f has a simple pole at a, then a is a branch point of f. (The converse need not be true).
A non-removable singularity that is not a pole or a branch point is called an essential singularity.
A complex function which is holomorphic except for some isolated singularities and whose only singularities are poles is called meromorphic.
