Girish Mahajan (Editor)

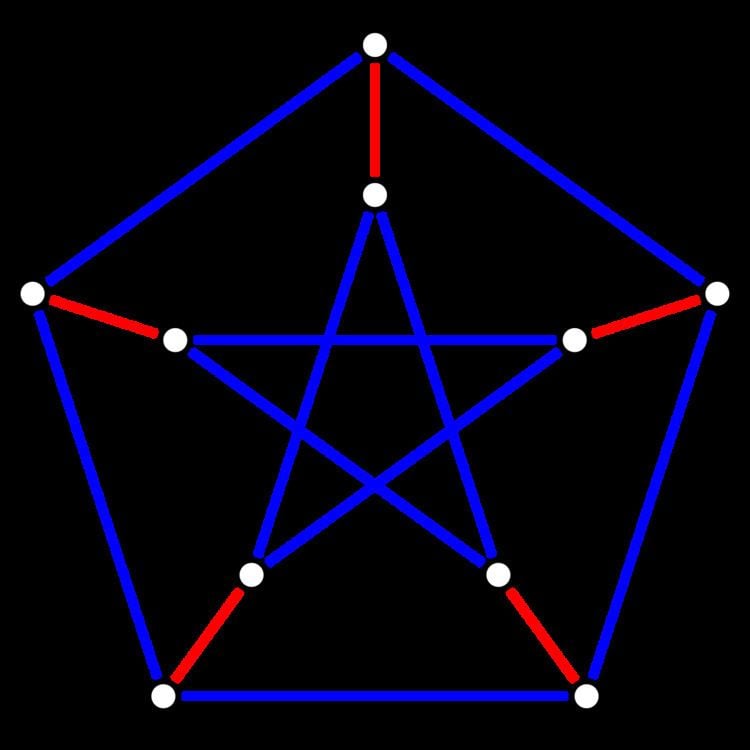
Petersen's theorem

Updated on
Edit
Like
Comment
Share on FacebookTweet on TwitterShare on LinkedInShare on Reddit
Petersen's theorem

In the mathematical discipline of graph theory, Petersen's theorem, named after Julius Petersen, is one of the earliest results in graph theory and can be stated as follows:

Contents

Petersen's Theorem. Every cubic, bridgeless graph contains a perfect matching.

In other words, if a graph has exactly three edges at each vertex, and every edge belongs to a cycle, then it has a set of edges that touches every vertex exactly once.

Proof

We show that for every cubic, bridgeless graph G = (V, E) we have that for every set U ⊆ V the number of connected components in the graph induced by V − U with an odd number of vertices is at most the cardinality of U. Then by Tutte theorem G contains a perfect matching.

Let Gi be a component with an odd number of vertices in the graph induced by the vertex set V − U. Let Vi denote the vertices of Gi and let mi denote the number of edges of G with one vertex in Vi and one vertex in U. By a simple double counting argument we have that

∑ v ∈ V i deg G ⁡ ( v ) = 2 | E i | + m i ,

where Ei is the set of edges of Gi with both vertices in Vi. Since

∑ v ∈ V i deg G ⁡ ( v ) = 3 | V i |

is an odd number and 2|Ei| is an even number it follows that mi has to be an odd number. Moreover, since G is bridgeless we have that mi ≥ 3.

Let m be the number of edges in G with one vertex in U and one vertex in the graph induced by V − U. Every component with an odd number of vertices contributes at least 3 edges to m, and these are unique, therefore, the number of such components is at most m/3. In the worst case, every edge with one vertex in U contributes to m, and therefore m ≤ 3|U|. We get

| U | ≥ 1 3 m ≥ | { components with an odd number of vertices } | ,

which shows that the condition of Tutte theorem holds.

History

The theorem is due to Julius Petersen, a Danish mathematician. It can be considered as one of the first results in graph theory. The theorem appears first in the 1891 article "Die Theorie der regulären graphs". By today's standards Petersen's proof of the theorem is complicated. A series of simplifications of the proof culminated in the proofs by Frink (1926) and König (1936).

In modern textbooks Petersen's theorem is covered as an application of Tutte's theorem.

Applications

  • In a cubic graph with a perfect matching, the edges that are not in the perfect matching form a 2-factor. By orienting the 2-factor, the edges of the perfect matching can be extended to paths of length three, say by taking the outward-oriented edges. This shows that every cubic, bridgeless graph decomposes into edge-disjoint paths of length three.
  • Petersen's theorem can also be applied to show that every maximal planar graph can be decomposed into a set of edge-disjoint paths of length three. In this case, the dual graph is cubic and bridgeless, so by Petersen's theorem it has a matching, which corresponds in the original graph to a pairing of adjacent triangle faces. Each pair of triangles gives a path of length three that includes the edge connecting the triangles together with two of the four remaining triangle edges.
  • By applying Petersen's theorem to the dual graph of a triangle mesh and connecting pairs of triangles that are not matched, one can decompose the mesh into cyclic strips of triangles. With some further transformations it can be turned into a single strip, and hence gives a method for transforming a triangle mesh such that its dual graph becomes hamiltonian.

    • Number of perfect matchings in cubic bridgeless graphs

    It was conjectured by Lovász and Plummer that the number of perfect matchings contained in a cubic, bridgeless graph is exponential in the number of the vertices of the graph n. The conjecture was first proven for bipartite, cubic, bridgeless graphs by Voorhoeve (1979), later for planar, cubic, bridgeless graphs by Chudnovsky & Seymour (2012). The general case was settled by Esperet et al. (2011), where it was shown that every cubic, bridgeless graph contains at least 2 n / 3656 perfect matchings.

    Algorithmic versions

    Biedl et al. (2001) discuss efficient versions of Petersen's theorem. Based on Frink's proof they obtain an O(n log4 n) algorithm for computing a perfect matching in a cubic, bridgeless graph with n vertices. If the graph is furthermore planar the same paper gives an O(n) algorithm. Their O(n log4 n) time bound can be improved based on subsequent improvements to the time for maintaining the set of bridges in a dynamic graph. Further improvements, reducing the time bound to O(n log2 n) or (with additional randomized data structures) O(n log n (log log n)3), were given by Diks & Stanczyk (2010).

    Higher degree

    If G is a regular graph of degree d whose edge connectivity is at least d − 1, and G has an even number of vertices, then it has a perfect matching. More strongly, every edge of G belongs to at least one perfect matching. The condition on the number of vertices can be omitted from this result when the degree is odd, because in that case (by the handshaking lemma) the number of vertices is always even.

    References

    Petersen's theorem Wikipedia
    (Text) CC BY-SA


    Similar Topics