Pascal's simplex

Generic Pascal's m-simplex

Let m (m > 0) be a number of terms of a polynomial and n (n ≥ 0) be a power the polynomial is raised to.

Let ∧ m denote a Pascal's m-simplex. Each Pascal's m-simplex is a semi-infinite object, which consists of an infinite series of its components.

Let ∧ n m denote its n^th component, itself a finite (m − 1)-simplex with the edge length n, with a notational equivalent △ n m − 1 .

nth component

∧ n m = △ n m − 1 consists of the coefficients of multinomial expansion of a polynomial with m terms raised to the power of n:

| x | n = ∑ | k | = n ( n k ) x k ;     x ∈ R m ,   k ∈ N 0 m ,   n ∈ N 0 ,   m ∈ N

where | x | = ∑ i = 1 m x i ,   | k | = ∑ i = 1 m k i ,   x k = ∏ i = 1 m x i k i .

Example for ∧ 4 {displaystyle wedge ^{4}}

Pascal's 4-simplex (sequence A189225 in the OEIS), sliced along the k₄. All points of the same color belong to the same n-th component, from red (for n = 0) to blue (for n = 3).

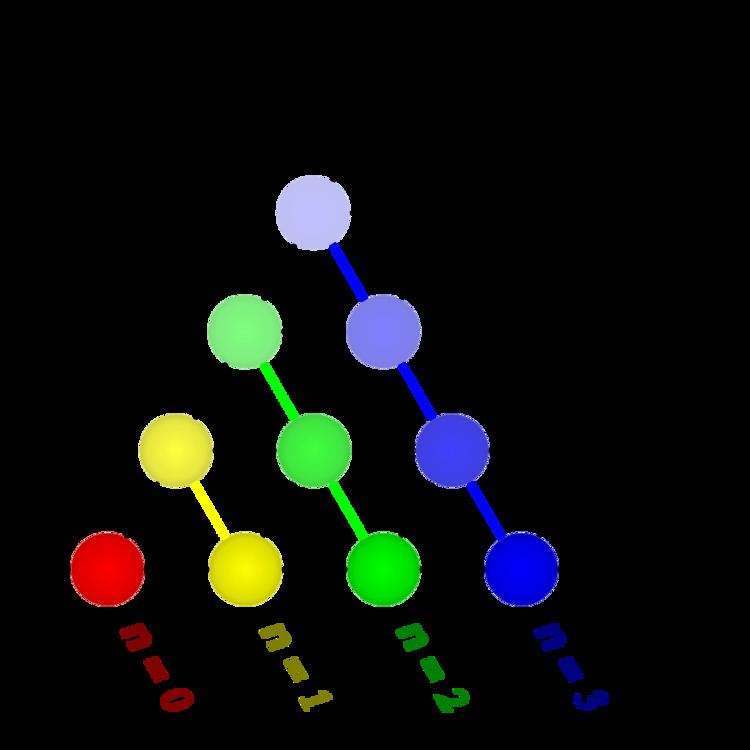
Pascal's 1-simplex

∧ 1 is not known by any special name.

nth component

∧ n 1 = △ n 0 (a point) is the coefficient of multinomial expansion of a polynomial with 1 term raised to the power of n:

( x 1 ) n = ∑ k 1 = n ( n k 1 ) x 1 k 1 ;     k 1 , n ∈ N 0

Arrangement of △ n 0

( n n )

which equals 1 for all n.

Pascal's 2-simplex

∧ 2 is known as Pascal's triangle (sequence A007318 in the OEIS).

nth component

∧ n 2 = △ n 1 (a line) consists of the coefficients of binomial expansion of a polynomial with 2 terms raised to the power of n:

( x 1 + x 2 ) n = ∑ k 1 + k 2 = n ( n k 1 , k 2 ) x 1 k 1 x 2 k 2 ;     k 1 , k 2 , n ∈ N 0

Arrangement of △ n 1

( n n , 0 ) , ( n n − 1 , 1 ) , ⋯ , ( n 1 , n − 1 ) , ( n 0 , n )

Pascal's 3-simplex

∧ 3 is known as Pascal's tetrahedron (sequence A046816 in the OEIS).

nth component

∧ n 3 = △ n 2 (a triangle) consists of the coefficients of trinomial expansion of a polynomial with 3 terms raised to the power of n:

( x 1 + x 2 + x 3 ) n = ∑ k 1 + k 2 + k 3 = n ( n k 1 , k 2 , k 3 ) x 1 k 1 x 2 k 2 x 3 k 3 ;     k 1 , k 2 , k 3 , n ∈ N 0

Arrangement of △ n 2

( n n , 0 , 0 ) , ( n n − 1 , 1 , 0 ) , ⋯ ⋯ , ( n 1 , n − 1 , 0 ) , ( n 0 , n , 0 ) ( n n − 1 , 0 , 1 ) , ( n n − 2 , 1 , 1 ) , ⋯ ⋯ , ( n 0 , n − 1 , 1 ) ⋮ ( n 1 , 0 , n − 1 ) , ( n 0 , 1 , n − 1 ) ( n 0 , 0 , n )

Inheritance of components

∧ n m = △ n m − 1 is numerically equal to each (m − 1)-face (there is m + 1 of them) of △ n m = ∧ n m + 1 , or:

∧ n m = △ n m − 1 ⊂   △ n m = ∧ n m + 1

From this follows, that the whole ∧ m is (m + 1)-times included in ∧ m + 1 , or:

∧ m ⊂ ∧ m + 1

Example

∧ 1 ∧ 2 ∧ 3 ∧ 4 ∧ 0 m 1 1 1 1 ∧ 1 m 1 1 1 1 1 1 1 1 1 1 ∧ 2 m 1 1 2 1 1 2 1 1 2 1 2 2 1 2 2 2 2 2 1 1 ∧ 3 m 1 1 3 3 1 1 3 3 1 1 3 3 1 3 6 3 3 3 1 3 6 3 3 6 3 6 6 3 3 3 3 3 3 1 1

For more terms in the above array refer to (sequence A191358 in the OEIS)

Equality of sub-faces

Conversely, ∧ n m + 1 = △ n m is (m + 1)-times bounded by △ n m − 1 = ∧ n m , or:

∧ n m + 1 = △ n m ⊃ △ n m − 1 = ∧ n m

From this follows, that for given n, all i-faces are numerically equal in n^th components of all Pascal's (m > i)-simplices, or:

∧ n i + 1 = △ n i ⊂ △ n m > i = ∧ n m > i + 1

Example

The 3rd component (2-simplex) of Pascal's 3-simplex is bounded by 3 equal 1-faces (lines). Each 1-face (line) is bounded by 2 equal 0-faces (vertices):

2-simplex 1-faces of 2-simplex 0-faces of 1-face 1 3 3 1 1 . . . . . . 1 1 3 3 1 1 . . . . . . 1 3 6 3 3 . . . . 3 . . . 3 3 3 . . 3 . . 1 1 1 .

Also, for all m and all n:

1 = ∧ n 1 = △ n 0 ⊂ △ n m − 1 = ∧ n m

Number of coefficients

For the n^th component ((m − 1)-simplex) of Pascal's m-simplex, the number of the coefficients of multinomial expansion it consists of is given by:

( ( n − 1 ) + ( m − 1 ) ( m − 1 ) ) + ( n + ( m − 2 ) ( m − 2 ) ) = ( n + ( m − 1 ) ( m − 1 ) ) ,

that is, either by a sum of the number of coefficients of an (n − 1)^th component ((m − 1)-simplex) of Pascal's m-simplex with the number of coefficients of an n^th component ((m − 2)-simplex) of Pascal's (m − 1)-simplex, or by a number of all possible partitions of an n^th power among m exponents.

Example

Interestingly, the terms of this table comprise a Pascal triangle in the format of a symmetric Pascal matrix.

Symmetry

(An n^th component ((m − 1)-simplex) of Pascal's m-simplex has the (m!)-fold spatial symmetry.)

Geometry

(Orthogonal axes k_1 ... k_m in m-dimensional space, vertices of component at n on each axe, the tip at [0,...,0] for n=0.)

Numeric construction

(Wrapped n-th power of a big number gives instantly the n-th component of a Pascal's simplex.)

| b d p | n = ∑ | k | = n ( n k ) b d p ⋅ k ;     b , d ∈ N ,   n ∈ N 0 ,   k , p ∈ N 0 m ,   p :   p 1 = 0 , p i = ( n + 1 ) i − 2

where b d p = ( b d p 1 , ⋯ , b d p m ) ∈ N m ,   p ⋅ k = ∑ i = 1 m p i k i ∈ N 0 .