 | ||
The painter's algorithm, also known as a priority fill, is one of the simplest solutions to the visibility problem in 3D computer graphics. When projecting a 3D scene onto a 2D plane, it is necessary at some point to decide which polygons are visible, and which are hidden.
The name "painter's algorithm" refers to the technique employed by many painters of painting distant parts of a scene before parts which are nearer thereby covering some areas of distant parts. The painter's algorithm sorts all the polygons in a scene by their depth and then paints them in this order, farthest to closest. It will paint over the parts that are normally not visible — thus solving the visibility problem — at the cost of having painted invisible areas of distant objects. The ordering used by the algorithm is called a 'depth order', and does not have to respect the numerical distances to the parts of the scene: the essential property of this ordering is, rather, that if one object obscures part of another then the first object is painted after the object that it obscures. Thus, a valid ordering can be described as a topological ordering of a directed acyclic graph representing occlusions between objects.
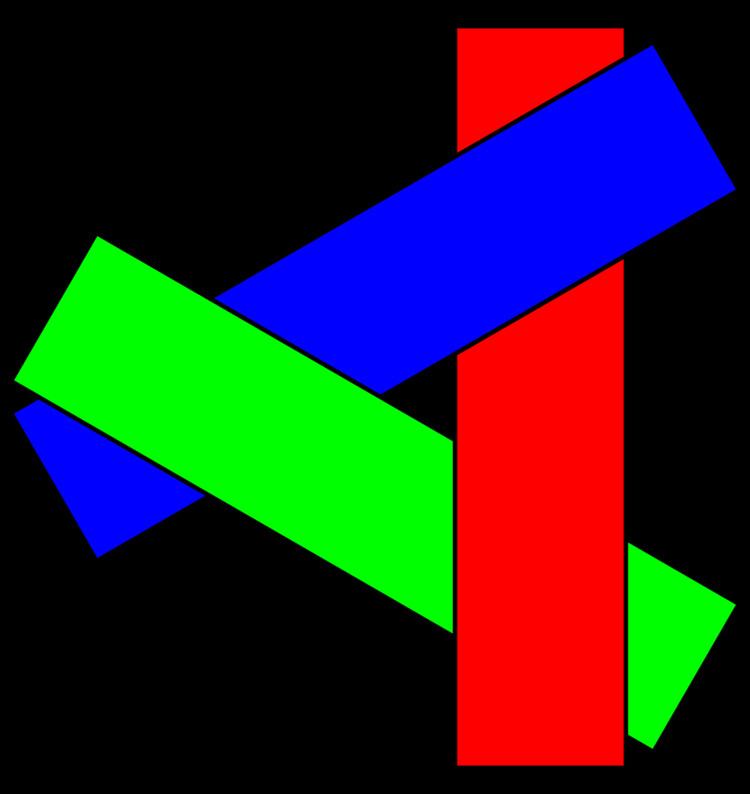
The algorithm can fail in some cases, including cyclic overlap or piercing polygons. In the case of cyclic overlap, as shown in the figure to the right, Polygons A, B, and C overlap each other in such a way that it is impossible to determine which polygon is above the others. In this case, the offending polygons must be cut to allow sorting. Newell's algorithm, proposed in 1972, provides a method for cutting such polygons. Numerous methods have also been proposed in the field of computational geometry.
The case of piercing polygons arises when one polygon intersects another. As with cyclic overlap, this problem may be resolved by cutting the offending polygons.
In basic implementations, the painter's algorithm can be inefficient. It forces the system to render each point on every polygon in the visible set, even if that polygon is occluded in the finished scene. This means that, for detailed scenes, the painter's algorithm can overly tax the computer hardware.
A reverse painter's algorithm is sometimes used, in which objects nearest to the viewer are painted first — with the rule that paint must never be applied to parts of the image that are already painted (unless they are partially transparent). In a computer graphic system, this can be very efficient, since it is not necessary to calculate the colors (using lighting, texturing and such) for parts of much distant scene that are hidden by nearby objects. However, the reverse algorithm suffers from many of the same problems as the standard version.
These and other flaws with the algorithm led to the development of Z-buffer techniques, which can be viewed as a development of the painter's algorithm, by resolving depth conflicts on a pixel-by-pixel basis, reducing the need for a depth-based rendering order. Even in such systems, a variant of the painter's algorithm is sometimes employed. As Z-buffer implementations generally rely on fixed-precision depth-buffer registers implemented in hardware, there is scope for visibility problems due to rounding error. These are overlaps or gaps at joints between polygons. To avoid this, some graphics engine implementations "overrender", drawing the affected edges of both polygons in the order given by painter's algorithm. This means that some pixels are actually drawn twice (as in the full painter's algorithm) but this happens on only small parts of the image and has a negligible performance effect.
