 | ||
Network operator matrix (NOM) is a representation of mathematical expressions in computer memory.
NOM is a new approach to the problem of automatic search of mathematical equations. The researcher defines the sets of operations, variables and parameters. The computer program generates a number of mathematical equations that satisfy given restrictions. Then the optimization algorithm finds the structure of appropriate mathematical expression and its parameters.
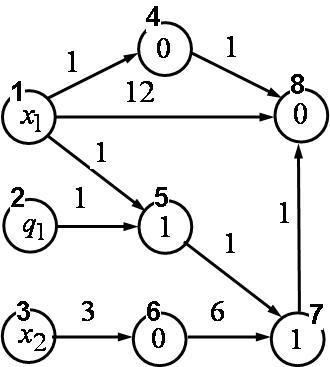
Network operator is a directed graph that corresponds to some mathematical expressions. Every source nodes of the graph are variables or constants of mathematical expression, inner nodes correspond to binary operations and edges correspond to unary operations. The calculation’s result of mathematical expression is kept in the last sink node.
Example
Consider the following mathematical expression
The graph for Expression (1), is presented in Fig. 1.
On the edges we place unary operations
In the inner and sink nodes we place binary operations
Expression 1 can be presented in the PC memory as a NOM
Any mathematical expression can be presented as a network operator matrix.
To calculate the mathematical expression by the network operator matrix the node vector is used.
Each component of node vector corresponds to the nodes of the network operator graph. Initially each component is equal to the argument for the given node or the unit element of binary operation.
For addition and multiplication the number of operation equals its unit element. For addition it is 0, for multiplication it is 1. The node vector for the given example
The calculation by matrix
Follow the rows of the matrix.
For the Row 1 we have
Take arguments from
Further in Row 1 we have
As a result after Row 1 we have
For the Row 2 we have
then follow the rows
