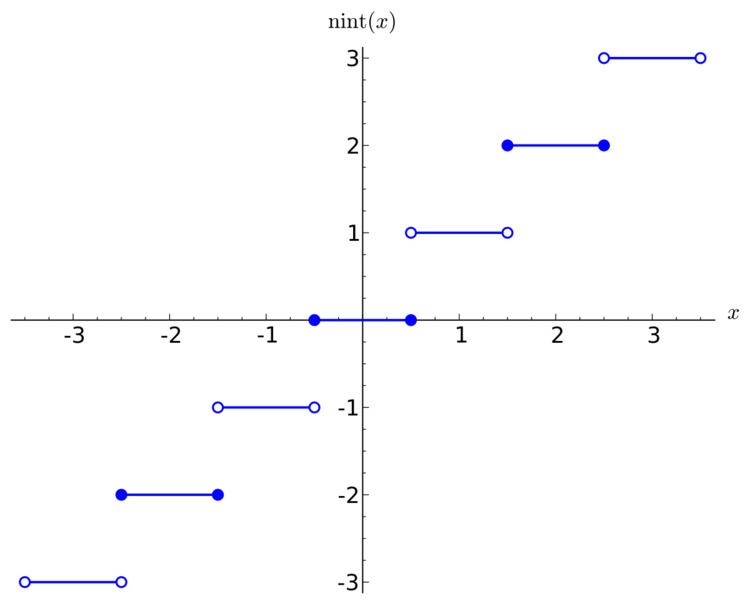
In computer science, the nearest integer function of real number x denoted variously by
[
x
]
,
⌊
x
⌉
,
∥
x
∥
, nint(x), or Round(x), is a function which returns the nearest integer to x. To avoid ambiguity when operating on half-integers, a rounding rule must be chosen. On most computer implementations, the selected rule is to round half-integers to the nearest even integer—for example,
[
1.25
]
=
1
[
1.50
]
=
2
[
1.75
]
=
2
[
2.25
]
=
2
[
2.50
]
=
2
[
2.75
]
=
3
[
3.25
]
=
3
[
3.50
]
=
4
[
3.75
]
=
4
[
4.50
]
=
4
etc.
This is in accordance with the IEEE 754 standards and helps reduce bias in the result.
There are many other possible rules for tie breaking when rounding a half integer include rounding up, rounding down, rounding to or away from zero, or random rounding up or down.