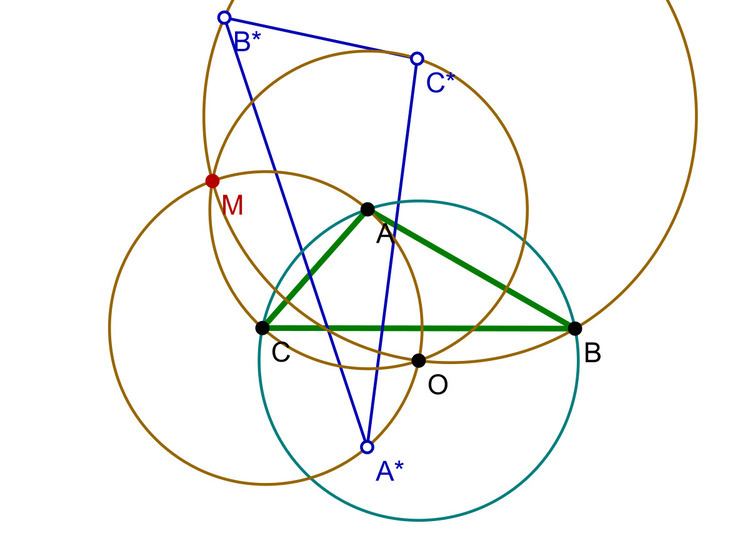
In Euclidean geometry, Musselman's theorem is a property of certain circles defined by an arbitrary triangle.
Specifically, let T be a triangle, and A , B , and C its vertices. Let A ∗ , B ∗ , and C ∗ be the vertices of the reflection triangle T ∗ , obtained by mirroring each vertex of T across the opposite side. Let O be the circumcenter of T . Consider the three circles S A , S B , and S C defined by the points A O A ∗ , B O B ∗ , and C O C ∗ , respectively. The theorem says that these three Musselman circles meet in a point M , that is the inverse with respect to the circumcenter of T of the isogonal conjugate or the nine-point center of T .
The common point M is the Gilbert point of T , which is point X 1157 in Clark Kimberling's list of triangle centers.
The theorem was proposed as an advanced problem by J. R. Musselman and R. Goormaghtigh in 1939, and a proof was presented by them in 1941. A generalization of this result was stated and proved by Goormaghtigh.
The generalization of Musselman's theorem by Goormaghtigh does not mention the circles explicitly.
As before, let A , B , and C be the vertices of a triangle T , and O its circumcenter. Let H be the orthocenter of T , that is, the intersection of its three altitude lines. Let A ′ , B ′ , and C ′ be three points on the segments O A , O B , and O C , such that O A ′ / O A = O B ′ / O B = O C ′ / O C = t . Consider the three lines L A , L B , and L C , perpendicular to O A , O B , and O C though the points A ′ , B ′ , and C ′ , respectively. Let P A , P B , and P C be the intersections of these perpendicular with the lines B C , C A , and A B , respectively.
It had been observed by J. Neuberg, in 1884, that the three points P A , P B , and P C lie on a common line R . Let N be the projection of the circumcenter O on the line R , and N ′ the point on O N such that O N ′ / O N = t . Goormaghtigh proved that N ′ is the inverse with respect to the circumcircle of T of the isogonal conjugate of the point Q on the Euler line O H , such that Q H / Q O = 2 t .