 | ||
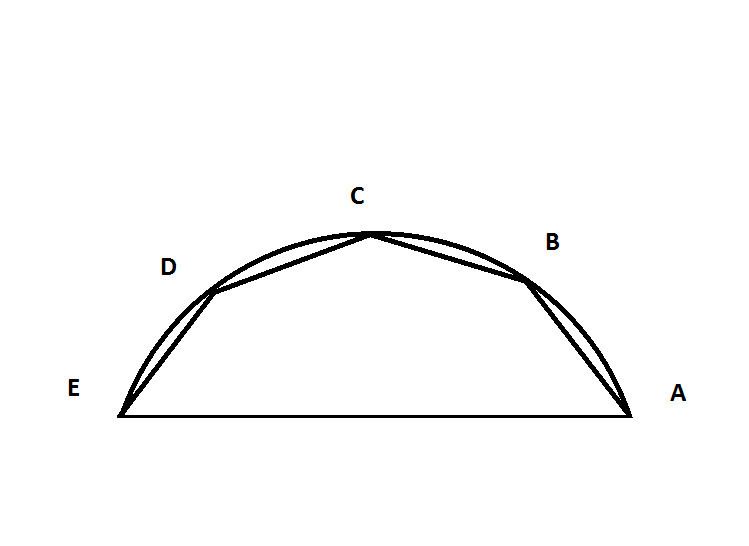
Ming Antu's infinite series expansion of trigonometric functions. Ming Antu, a court mathematician of the Qing dynasty did extensive work on infinite series expansion of trigonometric functions in his masterpiece Geyuan Milv Jifa(Quick Method of Dissecting the Circle and Determination of The Precise Ratio of the Circe). Ming Antu built geometrical models based on a major arc of a circle and nth dissection of the major arc. In Fig 1, AE is the major chord of arc ABCDE, and AB, BC, CD, DE are its nth equal segments. If chord AE = y, chord AB = BC = CD = DE = x, find chord y as infinite series expansion of chord x. He studied the cases of n = 2, 3, 4, 5, 10, 100, 1000 and 10000 in great detail in vol 3 and vol 4 of Geyuan Milv Jifa.
Contents
Historical background
In 1701, French Jesuit missionary(Pierre Jartoux 1668-1720) came to China, he brought along three infinite series expansion of trigonometry functions by Isaac Newton and J. Gregory:
These infinite series stirred up great interest among Chinese mathematicians,as calculation of π with these "quick methods" involve only multiplication, addition or subtraction, much faster than classic Liu Hui's π algorithm which involves taking square roots. However, Jartoux did not bring along the method for deriving these infinite series.Ming Antu suspected that the westerner did not want to share their secret,hence he set to work on it, and spent on and off for thirty years and completed a manuscript Geyuan Milv Jifa, he created geometrical models for obtaining trigonometric infinite series, and not only found the method for deriving the above three infinite series, but also discovered six more infinite series. In the process, he discovered and applied Catalan number.
Two-segment chord
Figure 2 is Ming Antu's model of 2 segment chord. Arc BCD is a part of circle with unity radius. AD is the main chord, arc BCD is bissected at C, draw lines BC, CD, let BC = CD = x and let radius AC = 1.
Apparently,
Let EJ = EF, FK = FJ; extend BE straight to L, and let EL = BE; make BF = BE, so F is inline with AE. Extended BF to M, let BF = MF; connect LM, LM apparently passes point C. The inverted triangle BLM along BM axis into triangle BMN, such that C coincident with G, and point L coincident with point N. The Invert triangle NGB along BN axis into triangle; apparently BI = BC.
BM bisects CG and let BM = BC; join GM, CM; draw CO = CM to intercept BM at O; make MP = MO; make NQ = NR, R is the intersection of BN and AC. ∠EBC = 1/2 ∠CAE = 1/2 ∠EAB;
So
and
Because kite-shaped ABEC and BLIN are similar,.
Thus
then
And so on
Add up the following two equations to eliminate
......................................
Expansion coefficients of the numerators: 1,1,2,5,14,42,132 ...... (see Figure II Ming Antu original figure bottom line, read from right to left) are none other than the Catalan numbers , Ming Antu is the first person in history to discover the Catalan number.
Thus :
in which
substituted into
Finally he obtained
In Figure 1 BAE angle = α, BAC angle = 2α
Ming Antu obtained
Three-segment chord
As shown in Fig 3,BE is a whole arc chord, BC = CE = DE = a are three arcs of equal portions. Radii AB = AC = AD = AE = 1. Draw lines BC, CD, DE, BD, EC; let BG=EH = BC, Bδ = Eα = BD, then triangle Cαβ = Dδγ; while triangle Cαβ is similar to triangle BδD.
As such:
Eventually, he obtained
Four-segment chord
Let
Five-segment chord
Ten-segment chord
From here on, Ming Antu stop building geometrical model, he carried out his computation by pure algebraic manipulation of infinite series.
Apparently ten segments can be considered as a composite 5 segment, with each segment in turn consist of two subsegments.
He computed the third and fifth power of infinite series
Hundred-segment chord
A hundred segment arc's chord can be considered as composite 10 segment-10 subsegments, thus sustutde
Thousand-segment chord
Ten-thousand-segment chord
When number of segments approaches infinity
After obtained the infinite series for n=2,3,5,10,100,1000,10000 segments, Ming Antu went on to handle the case when n approaches infinity.
y100,y1000 and y10000 can be rewritten as:
He noted that obviously, when n approaches infinity, the denominators 24.000000240000002400,24.000002400000218400*80 approach 24 and 24*80 respectively, and when n -> infinity, na (100a,1000a,1000a)becomes the length of the arc; hence
Ming Antu then performed an infinite series reversion and expressed the arc in terms of its chord
