The Meyer wavelet is an orthogonal wavelet proposed by Yves Meyer. It is infinitely differentiable with infinite support and defined in frequency domain in terms of function ν as:
Ψ ( ω ) := { 1 2 π sin ( π 2 ν ( 3 | ω | 2 π − 1 ) ) e j ω / 2 if 2 π / 3 < | ω | < 4 π / 3 , 1 2 π cos ( π 2 ν ( 3 | ω | 4 π − 1 ) ) e j ω / 2 if 4 π / 3 < | ω | < 8 π / 3 , 0 otherwise , where:
ν ( x ) := { 0 if x < 0 , x if 0 < x < 1 , 1 if x > 1. There are many different ways for defining this auxiliary function, which yields variants of the Meyer wavelet. For instance, another standard implementation adopts
ν ( x ) := { x 4 ( 35 − 84 x + 70 x 2 − 20 x 3 ) if 0 < x < 1 , 0 otherwise . The Meyer scale function is given by:
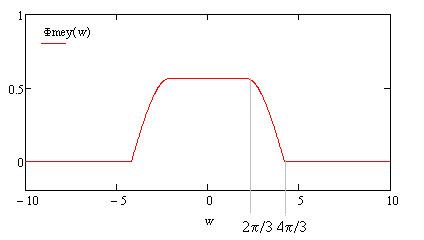
Φ ( ω ) := { 1 2 π if | ω | < 2 π / 3 , 1 2 π cos ( π 2 ν ( 3 | ω | 2 π − 1 ) ) if 2 π / 3 < | ω | < 4 π / 3 , 0 otherwise . In the time-domain, the waveform of the Meyer mother-wavelet has the shape as shown in the following figure:
In 2015, Victor Vermehren Valenzuela and H. M. de Oliveira gave the explicitly expressions of Meyer wavelet and scale functions:
ϕ ( t ) = { 2 3 + 4 3 π t = 0 , sin ( 2 π 3 t ) + 4 3 t cos ( 4 π 3 t ) π t − 16 π 9 t 3 o t h e r w i s e ,
and
ψ ( t ) = ψ 1 ( t ) + ψ 2 ( t )
where
ψ 1 ( t ) = 4 3 π ( t − 1 2 ) cos [ 2 π 3 ( t − 1 2 ) ] − 1 π sin [ 4 π 3 ( t − 1 2 ) ] ( t − 1 2 ) − 16 9 ( t − 1 2 ) 3 ,
and
ψ 2 ( t ) = 8 3 π ( t − 1 2 ) cos [ 8 π 3 ( t − 1 2 ) ] + 1 π sin [ 4 π 3 ( t − 1 2 ) ] ( t − 1 2 ) − 64 9 ( t − 1 2 ) 3 .