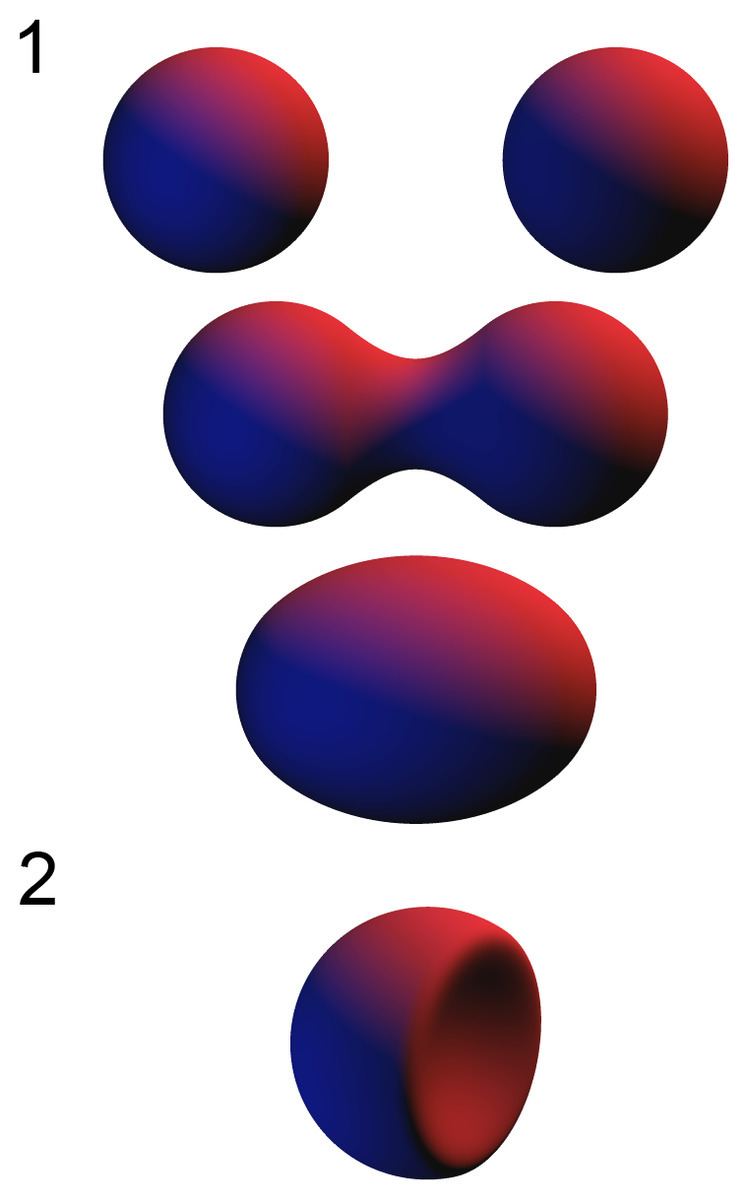
Metaballs

Metaballs are, in computer graphics, organic-looking n-dimensional objects. The technique for rendering metaballs was invented by Jim Blinn in the early 1980s.

Each metaball is defined as a function in n-dimensions (i.e. for three dimensions, f ( x , y , z ) ; three-dimensional metaballs tend to be most common, with two-dimensional implementations popular as well). A thresholding value is also chosen, to define a solid volume. Then,

represents whether the volume enclosed by the surface defined by n metaballs is filled at ( x , y , z ) or not.

A typical function chosen for metaballs is f ( x , y , z ) = 1 / ( ( x − x 0 ) 2 + ( y − y 0 ) 2 + ( z − z 0 ) 2 ) , where ( x 0 , y 0 , z 0 ) is the center of the metaball. However, due to the divide, it is computationally expensive. For this reason, approximate polynomial functions are typically used.

When seeking a more efficient falloff function, several qualities are desired:

The simplest falloff curve that satisfies these criteria is: f ( r ) = ( 1 − r 2 ) 2 , where r is the distance to the point. This formulation avoids expensive square root calls.

More complicated models use a Gaussian potential constrained to a finite radius or a mixture of polynomials to achieve smoothness. The Soft Object model by the Wyvill brothers provides higher degree of smoothness and still avoids square roots.

A simple generalization of metaballs is to apply the falloff curve to distance-from-lines or distance-from-surfaces.

There are a number of ways to render the metaballs to the screen. In the case of three dimensional metaballs, the two most common are brute force raycasting and the marching cubes algorithm.

2D metaballs were a very common demo effect in the 1990s. The effect is also available as an XScreensaver module.