Meander (mathematics)

Meander

Given a fixed oriented line L in the Euclidean plane R², a meander of order n is a non-self-intersecting closed curve in R² which transversally intersects the line at 2n points for some positive integer n. The line and curve together form a meandric system. Two meanders are said to be equivalent if there is a homeomorphism of the whole plane that takes L to itself and takes one meander to the other.

Examples

The meander of order 1 intersects the line twice:

The meanders of order 2 intersect the line four times:

Meandric numbers

The number of distinct meanders of order n is the meandric number M_n. The first fifteen meandric numbers are given below (sequence A005315 in the OEIS).

M₁ = 1 M₂ = 2 M₃ = 8 M₄ = 42 M₅ = 262 M₆ = 1828 M₇ = 13820 M₈ = 110954 M₉ = 933458 M₁₀ = 8152860 M₁₁ = 73424650 M₁₂ = 678390116 M₁₃ = 6405031050 M₁₄ = 61606881612 M₁₅ = 602188541928

Meandric permutations

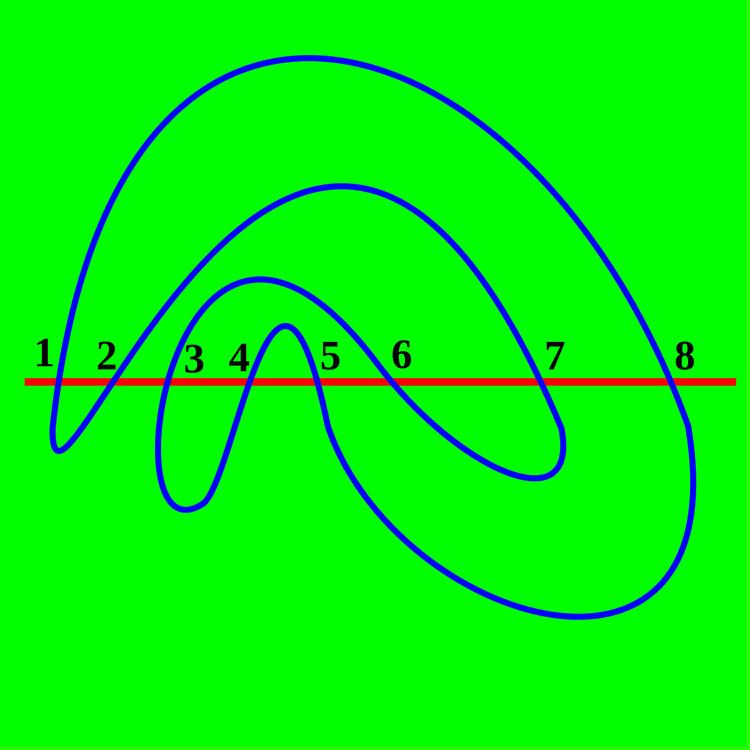
A meandric permutation of order n is defined on the set {1, 2, ..., 2n} and is determined by a meandric system in the following way:

With the line oriented from left to right, each intersection of the meander is consecutively labelled with the integers, starting at 1.

The curve is oriented upward at the intersection labelled 1.

The cyclic permutation with no fixed points is obtained by following the oriented curve through the labelled intersection points.

In the diagram on the right, the order 4 meandric permutation is given by (1 8 5 4 3 6 7 2). This is a permutation written in cyclic notation and not to be confused with one-line notation.

If π is a meandric permutation, then π² consists of two cycles, one containing of all the even symbols and the other all the odd symbols. Permutations with this property are called alternate permutations, since the symbols in the original permutation alternate between odd and even integers. However, not all alternate permutations are meandric because it may not be possible to draw them without introducing a self-intersection in the curve. For example, the order 3 alternate permutation, (1 4 3 6 5 2), is not meandric.

Open meander

Given a fixed oriented line L in the Euclidean plane R², an open meander of order n is a non-self-intersecting oriented curve in R² which transversally intersects the line at n points for some positive integer n. Two open meanders are said to be equivalent if they are homeomorphic in the plane.

Examples

The open meander of order 1 intersects the line once:

The open meander of order 2 intersects the line twice:

Open meandric numbers

The number of distinct open meanders of order n is the open meandric number m_n. The first fifteen open meandric numbers are given below (sequence A005316 in the OEIS).

m₁ = 1 m₂ = 1 m₃ = 2 m₄ = 3 m₅ = 8 m₆ = 14 m₇ = 42 m₈ = 81 m₉ = 262 m₁₀ = 538 m₁₁ = 1828 m₁₂ = 3926 m₁₃ = 13820 m₁₄ = 30694 m₁₅ = 110954

Semi-meander

Given a fixed oriented ray R in the Euclidean plane R², a semi-meander of order n is a non-self-intersecting closed curve in R² which transversally intersects the ray at n points for some positive integer n. Two semi-meanders are said to be equivalent if they are homeomorphic in the plane.

Examples

The semi-meander of order 1 intersects the ray once:

The semi-meander of order 2 intersects the ray twice:

Semi-meandric numbers

The number of distinct semi-meanders of order n is the semi-meandric number M_n (usually denoted with an overline instead of an underline). The first fifteen semi-meandric numbers are given below (sequence A000682 in the OEIS).

M₁ = 1 M₂ = 1 M₃ = 2 M₄ = 4 M₅ = 10 M₆ = 24 M₇ = 66 M₈ = 174 M₉ = 504 M₁₀ = 1406 M₁₁ = 4210 M₁₂ = 12198 M₁₃ = 37378 M₁₄ = 111278 M₁₅ = 346846

Properties of meandric numbers

There is an injective function from meandric to open meandric numbers:

M_n = m_2n−1

Each meandric number can be bounded by semi-meandric numbers:

M_n ≤ M_n ≤ M_2n

For n > 1, meandric numbers are even:

M_n ≡ 0 (mod 2)