Mason's gain formula

Formula

The gain formula is as follows:

G = y out y in = ∑ k = 1 N G k Δ k Δ   Δ = 1 − ∑ L i + ∑ L i L j − ∑ L i L j L k + ⋯ + ( − 1 ) m ∑ ⋯ + ⋯

where:

Δ = the determinant of the graph.

y_in = input-node variable

y_out = output-node variable

G = complete gain between y_in and y_out

N = total number of forward paths between y_in and y_out

G_k = path gain of the kth forward path between y_in and y_out

L_i = loop gain of each closed loop in the system

L_iL_j = product of the loop gains of any two non-touching loops (no common nodes)

L_iL_jL_k = product of the loop gains of any three pairwise nontouching loops

Δ_k = the cofactor value of Δ for the k^th forward path, with the loops touching the k^th forward path removed. *

Definitions

Path: a continuous set of branches traversed in the direction that they indicate.

Forward path: A path from an input node to an output node in which no node is touched more than once.

Loop: A path that originates and ends on the same node in which no node is touched more than once.

Path gain: the product of the gains of all the branches in the path.

Loop gain: the product of the gains of all the branches in the loop.

Procedure

To use this technique,

1. Make a list of all forward paths, and their gains, and label these G_k.
2. Make a list of all the loops and their gains, and label these L_i (for i loops). Make a list of all pairs of non-touching loops, and the products of their gains (L_iL_j). Make a list of all pairwise non-touching loops taken three at a time (L_iL_jL_k), then four at a time, and so forth, until there are no more.
3. Compute the determinant Δ and cofactors Δ_k.
4. Apply the formula.

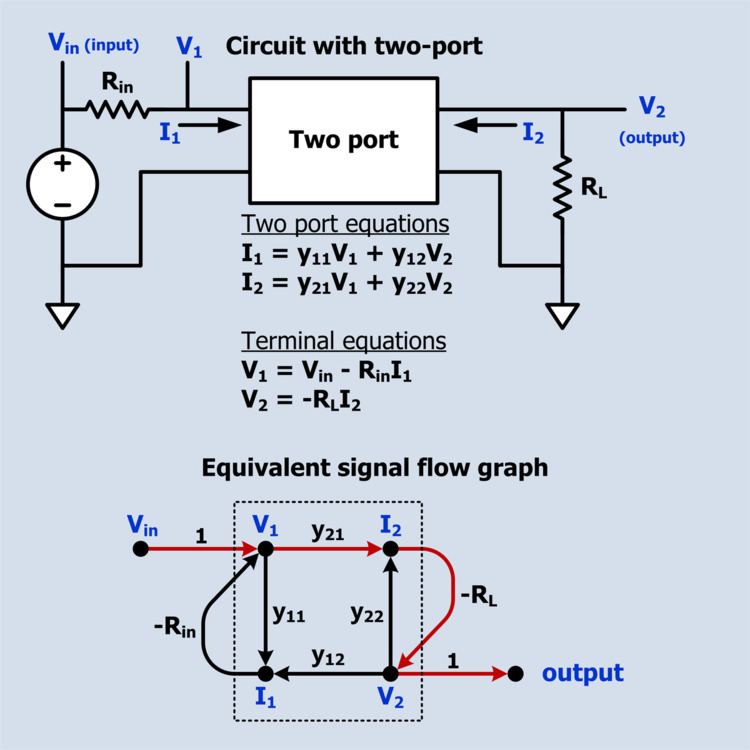
Circuit containing two-port

The transfer function from V_in to V₂ is desired.

There is only one forward path:

V_in to V₁ to I₂ to V₂ with gain G 1 = − y 21 R L

There are three loops:

V₁ to I₁ to V₁ with gain L 1 = − R i n y 11

V₂ to I₂ to V₂ with gain L 2 = − R L y 22

V₁ to I₂ to V₂ to I₁ to V₁ with gain L 3 = y 21 R L y 12 R i n

Δ = 1 − ( L 1 + L 2 + L 3 ) + ( L 1 L 2 ) note: L₁ and L₂ do not touch each other whereas L₃ touches both of the other loops. Δ 1 = 1 note: the forward path touches all the loops so all that is left is 1. G = G 1 Δ 1 Δ = − y 21 R L 1 + R i n y 11 + R L y 22 − y 21 R L y 12 R i n + R i n y 11 R L y 22

Digital IIR biquad filter

Digital filters are often diagramed as signal flow graphs.

There are two loops

L 1 = − a 1 Z − 1

L 2 = − a 2 Z − 2

Δ = 1 − ( L 1 + L 2 ) Note, the two loops touch so there is no term for their product.There are three forward paths

G 0 = b 0

G 1 = b 1 Z − 1

G 2 = b 2 Z − 2

All the forward paths touch all the loops so Δ 0 = Δ 1 = Δ 2 = 1 G = G 0 Δ 0 + G 1 Δ 1 + G 2 Δ 2 Δ G = b 0 + b 1 Z − 1 + b 2 Z − 2 1 + a 1 Z − 1 + a 2 Z − 2

Servo

The signal flow graph has six loops. They are:

L 0 = − β s M

L 1 = − ( R M + R S ) s L M

L 2 = − G M K M s 2 L M M

L 3 = − K C R S s L M

L 4 = − K V K C K M G T s 2 L M M

L 5 = − K P K V K C K M s 3 L M M

Δ = 1 − ( L 0 + L 1 + L 2 + L 3 + L 4 + L 5 ) + ( L 0 L 1 + L 0 L 3 )

There is one forward path:

g 0 = − K P K V K C K M s 3 L M M

The forward path touches all the loops therefore the co-factor Δ 0 = 1

And the gain from input to output is θ L θ C = g 0 Δ 0 Δ

Equivalent matrix form

Mason's rule can be stated in a simple matrix form. Assume T is the transient matrix of the graph where t n m = [ T ] n m is the sum transmittance of branches from node m toward node n. Then, the gain from node m to node n of the graph is equal to u n m = [ U ] n m , where

U = ( I − T ) − 1 ,

and I is the identity matrix.

Mason's Rule is also particularly useful for deriving the z-domain transfer function of discrete networks that have inner feedback loops embedded within outer feedback loops (nested loops). If the discrete network can be drawn as a signal flow graph, then the application of Mason's Rule will give that network's z-domain H(z) transfer function.

Complexity and Computational Applications

Mason's Rule can grow factorially, because the enumeration of paths in a directed graph grows thusly. To see this consider the complete directed graph on n vertices, having an edge between every pair of vertices. There is a path form y i n to y o u t for each of the ( n − 2 ) ! permutations of the intermediate vertices. Thus Gaussian elimination is more efficient in the general case.

Yet Mason's rule characterizes the transfer functions of interconnected systems in a way which is simultaneously algebraic and combinatorial, allowing for general statements and other computations in algebraic systems theory. While numerous inverses occur during Gaussian eliminiation, Mason's rule naturally collects these into a single quasi-inverse. General form is

Where as described above, q is a sum of cycle products, each of which typically falls into an ideal (for example, the strictly causal operators). Fractions of this form form a subring R ( 1 + ⟨ L i ⟩ ) − 1 of the rational function field. This observation carries over to the noncommutative case, even though Mason's rule itself must then be replaced by Riegle's rule.