Markov blanket

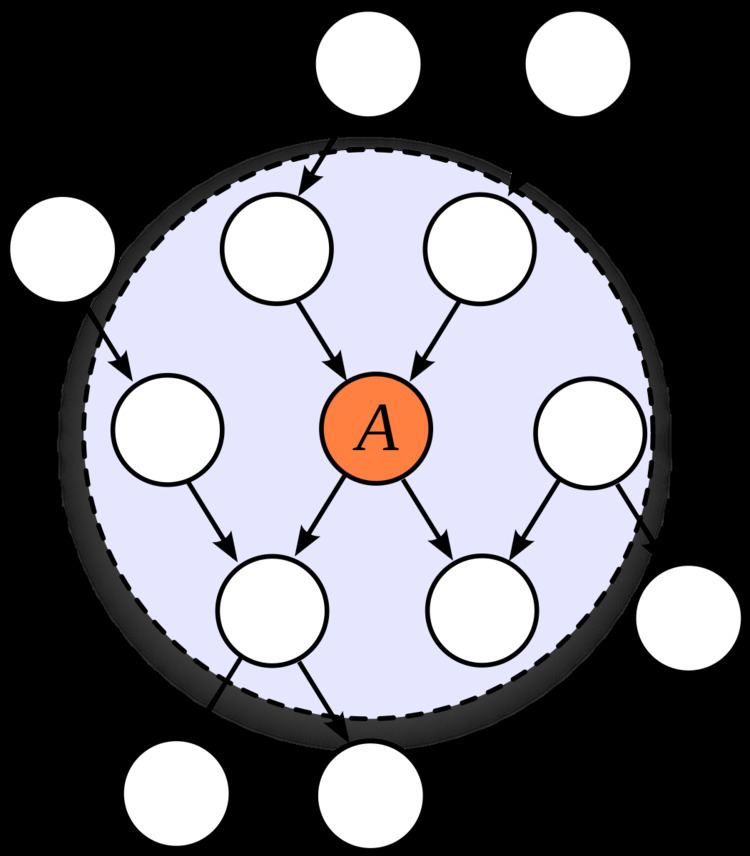
In machine learning, the Markov blanket for a node A in a Bayesian network is the set of nodes ∂ A composed of A 's parents, its children, and its children's other parents. In a Markov random field, the Markov blanket of a node is its set of neighboring nodes. A Markov blanket may also be denoted by M B ( A ) .

Every set of nodes in the network is conditionally independent of A when conditioned on the set ∂ A , that is, when conditioned on the Markov blanket of the node A . The probability has the Markov property; formally, for distinct nodes A and B :

The Markov blanket of a node contains all the variables that shield the node from the rest of the network. This means that the Markov blanket of a node is the only knowledge needed to predict the behavior of that node. The term was coined by Judea Pearl in 1988.

In a Bayesian network, the values of the parents and children of a node evidently give information about that node; however, its children's parents also have to be included, because they can be used to explain away the node in question. In a Markov random field, the Markov blanket for a node is simply its adjacent nodes.