Properties connected | ||
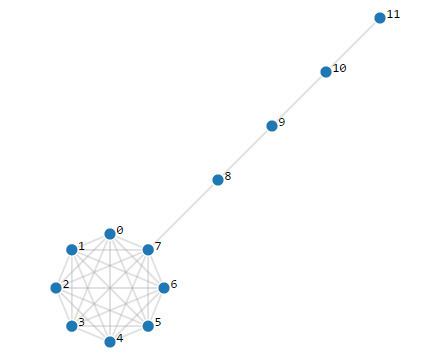 | ||
Vertices m + n {\displaystyle m+n} Edges ( m 2 ) + n {\displaystyle {\tbinom {m}{2}}+n} Girth { ∞ m ≤ 2 3 otherwise {\displaystyle \left\{{\begin{array}{ll}\infty &m\leq 2\\3&{\text{otherwise}}\end{array}}\right.} Notation L m , n {\displaystyle L_{m,n}} | ||
In the mathematical discipline of graph theory, the (m,n)-lollipop graph is a special type of graph consisting of a complete graph (clique) on m vertices and a path graph on n vertices, connected with a bridge.
The special case of the (2n/3,n/3)-lollipop graphs are known as graphs which achieve the maximum possible hitting time, cover time and commute time.
References
Lollipop graph Wikipedia(Text) CC BY-SA
