 | ||
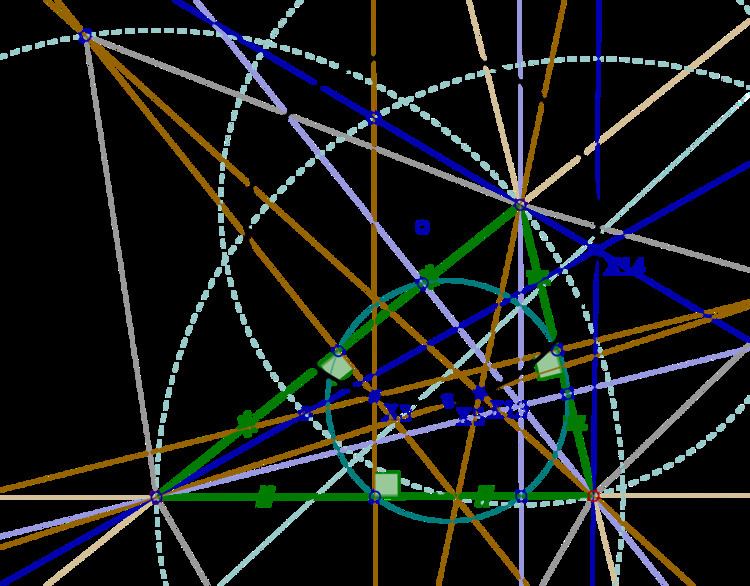
In Euclidean plane geometry, Lester's theorem, named after June Lester, states that in any scalene triangle, the two Fermat points, the nine-point center, and the circumcenter lie on the same circle.
Contents
Gibert's proof using the Kiepert hyperbola
Lester's circle theorem follows from a more general result by B. Gibert (2000); namely, that every circle whose diameter is a chord of the Kiepert hyperbola of the triangle and is perpendicular to its Euler line passes through the Fermat points.
Dao's lemma on the rectangular hyperbola
In 2014, Dao Thanh Oai showed that Gibert's result follows from a property of rectangular hyperbolas. Namely, let
Let
To get Lester's theorem from this result, take
Generalisation
A conjectured generalization of the Lester theorem was published in Encyclopedia of Triangle Centers as follows: Let
