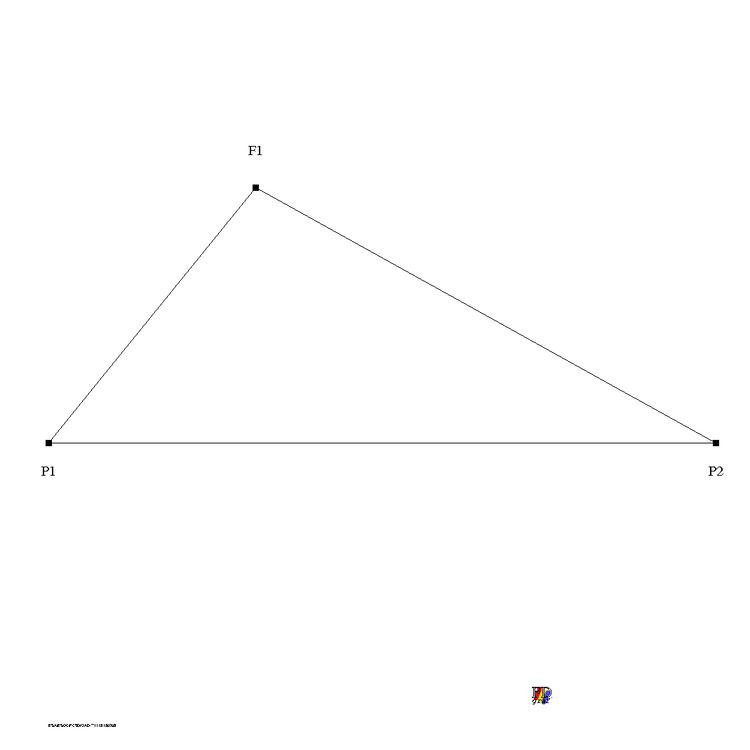
Lambert's problem - Alchetron, The Free Social Encyclopedia

In celestial mechanics Lambert's problem is concerned with the determination of an orbit from two position vectors and the time of flight, solved by Johann Heinrich Lambert. It has important applications in the areas of rendezvous, targeting, guidance, and preliminary orbit determination. Suppose a body under the influence of a central gravitational force is observed to travel from point P₁ on its conic trajectory, to a point P₂ in a time T. The time of flight is related to other variables by Lambert’s theorem, which states:

Initial geometrical analysis

The three points

F 1

The centre of attraction

P 1

The point corresponding to vector r ¯ 1

P 2

The point corresponding to vector r ¯ 2

form a triangle in the plane defined by the vectors r ¯ 1 and r ¯ 2 as illustrated in figure 1. The distance between the points P 1 and P 2 is 2 d , the distance between the points P 1 and F 1 is r 1 = r m − A and the distance between the points P 2 and F 1 is r 2 = r m + A . The value A is positive or negative depending on which of the points P 1 and P 2 that is furthest away from the point F 1 . The geometrical problem to solve is to find all ellipses that go through the points P 1 and P 2 and have a focus at the point F 1

The points F 1 , P 1 and P 2 define a hyperbola going through the point F 1 with foci at the points P 1 and P 2 . The point F 1 is either on the left or on the right branch of the hyperbola depending on the sign of A . The semi-major axis of this hyperbola is | A | and the eccentricity E is d | A | . This hyperbola is illustrated in figure 2.

Relative the usual canonical coordinate system defined by the major and minor axis of the hyperbola its equation is

x 2 A 2 − y 2 B 2 = 1 ( 1 )

with

B = | A | E 2 − 1 = d 2 − A 2 ( 2 )

For any point on the same branch of the hyperbola as F 1 the difference between the distances r 2 to point P 2 and r 1 to point P 1 is

r 2 − r 1 = 2 A ( 3 )

For any point F 2 on the other branch of the hyperbola corresponding relation is

s 1 − s 2 = 2 A ( 4 )

i.e.

r 1 + s 1 = r 2 + s 2 ( 5 )

But this means that the points P 1 and P 2 both are on the ellipse having the focal points F 1 and F 2 and the semi-major axis

a = r 1 + s 1 2 = r 2 + s 2 2 ( 6 )

The ellipse corresponding to an arbitrary selected point F 2 is displayed in figure 3.

Solution of Lambert's problem assuming an elliptic transfer orbit

First one separates the cases of having the orbital pole in the direction r ¯ 1 × r ¯ 2 or in the direction − r ¯ 1 × r ¯ 2 . In the first case the transfer angle α for the first passage through r ¯ 2 will be in the interval 0 < α < 180 ∘ and in the second case it will be in the interval 180 ∘ < α < 360 ∘ . Then r ¯ ( t ) will continue to pass through r ¯ 2 every orbital revolution.

In case r ¯ 1 × r ¯ 2 is zero, i.e. r ¯ 1 and r ¯ 2 have opposite directions, all orbital planes containing corresponding line are equally adequate and the transfer angle α for the first passage through r ¯ 2 will be 180 ∘ .

For any α with 0 < α < ∞ the triangle formed by P 1 , P 2 and F 1 are as in figure 1 with

d = r 1 2 + r 2 2 − 2 r 1 r 2 cos ⁡ α 2 ( 7 )

and the semi-major axis (with sign!) of the hyperbola discussed above is

A = r 2 − r 1 2 ( 8 )

The eccentricity (with sign!) for the hyperbola is

E = d A ( 9 )

and the semi-minor axis is

B = | A | E 2 − 1 = d 2 − A 2 ( 10 )

The coordinates of the point F 1 relative the canonical coordinate system for the hyperbola are (note that E has the sign of r 2 − r 1 )

x 0 = − r m E ( 11 ) y 0 = B ( x 0 A ) 2 − 1 ( 12 )

where

r m = r 2 + r 1 2 ( 13 )

Using the y-coordinate of the point F 2 on the other branch of the hyperbola as free parameter the x-coordinate of F 2 is (note that A has the sign of r 2 − r 1 )

x = A 1 + ( y B ) 2 ( 14 )

The semi-major axis of the ellipse passing through the points P 1 and P 2 having the foci F 1 and F 2 is

a = r 1 + s 1 2 = r 2 + s 2 2 = r m + E x 2 ( 15 )

The distance between the foci is

( x 0 − x ) 2 + ( y 0 − y ) 2 ( 16 )

and the eccentricity is consequently

e = ( x 0 − x ) 2 + ( y 0 − y ) 2 2 a ( 17 )

The true anomaly θ 1 at point P 1 depends on the direction of motion, i.e. if sin ⁡ α is positive or negative. In both cases one has that

cos ⁡ θ 1 = − ( x 0 + d ) f x + y 0 f y r 1 ( 18 )

where

f x = x 0 − x ( x 0 − x ) 2 + ( y 0 − y ) 2 ( 19 ) f y = y 0 − y ( x 0 − x ) 2 + ( y 0 − y ) 2 ( 20 )

is the unit vector in the direction from F 2 to F 1 expressed in the canonical coordinates.

If sin ⁡ α is positive then

sin ⁡ θ 1 = ( x 0 + d ) f y − y 0 f x r 1 ( 21 )

If sin ⁡ α is negative then

sin ⁡ θ 1 = − ( x 0 + d ) f y − y 0 f x r 1 ( 22 )

With

semi-major axis

eccentricity

initial true anomaly

being known functions of the parameter y the time for the true anomaly to increase with the amount α is also a known function of y. If t 2 − t 1 is in the range that can be obtained with an elliptic Kepler orbit corresponding y value can then be found using an iterative algorithm.

In the special case that r 1 = r 2 (or very close) A = 0 and the hyperbola with two branches deteriorates into one single line orthogonal to the line between P 1 and P 2 with the equation

x = 0 ( 1 ′ )

Equations (11) and (12) are then replaced with

x 0 = 0 ( 11 ′ ) y 0 = r m 2 − d 2 ( 12 ′ )

(14) is replaced by

x = 0 ( 14 ′ )

and (15) is replaced by

a = r m + d 2 + y 2 2 ( 15 ′ )

Numerical example

Assume the following values for an Earth centred Kepler orbit

r₁ = 10000 km

r₂ = 16000 km

α = 100°

These are the numerical values that correspond to figures 1, 2, and 3.

Selecting the parameter y as 30000 km one gets a transfer time of 3072 seconds assuming the gravitational constant to be μ = 398603 km³/s². Corresponding orbital elements are

semi-major axis = 23001 km

eccentricity = 0.566613

true anomaly at time t₁ = −7.577°

true anomaly at time t₂ = 92.423°

This y-value corresponds to Figure 3.

With

r₁ = 10000 km

r₂ = 16000 km

α = 260°

one gets the same ellipse with the opposite direction of motion, i.e.

true anomaly at time t₁ = 7.577°

true anomaly at time t₂ = 267.577° = 360° − 92.423°

and a transfer time of 31645 seconds.

The radial and tangential velocity components can then be computed with the formulas (see the Kepler orbit article)

V r = μ p ⋅ e ⋅ sin ⁡ θ V t = μ p ⋅ ( 1 + e ⋅ cos ⁡ θ ) .

The transfer times from P₁ to P₂ for other values of y are displayed in Figure 4.

Practical applications

The most typical use of this algorithm to solve Lambert's problem is certainly for the design of interplanetary missions. A spacecraft traveling from the Earth to for example Mars can in first approximation be considered to follow a heliocentric elliptic Kepler orbit from the position of the Earth at the time of launch to the position of Mars at the time of arrival. By comparing the initial and the final velocity vector of this heliocentric Kepler orbit with corresponding velocity vectors for the Earth and Mars a quite good estimate of the required launch energy and of the maneuvres needed for the capture at Mars can be obtained. This approach is often used in conjunction with the patched conic approximation. This is also a method for orbit determination. If two positions of a spacecraft at different times are known with good precision from for example a GPS fix the complete orbit can be derived with this algorithm, i.e. an interpolation and an extrapolation of these two position fixes is obtained.

Open source code to solve Lambert's problem

From MATLAB central

PyKEP a Python library for space flight mechanics and astrodynamics (contains a Lambert's solver, implemented in C++ and exposed to python via boost python)

References

Lambert's problem Wikipedia

(Text) CC BY-SA