The Kuhn length is a theoretical treatment, developed by Werner Kuhn, in which a real polymer chain is considered as a collection of N Kuhn segments each with a Kuhn length b . Each Kuhn segment can be thought of as if they are freely jointed with each other. Each segment in a freely jointed chain can randomly orient in any direction without the influence of any forces, independent of the directions taken by other segments. Instead of considering a real chain consisting of n bonds and with fixed bond angles, torsion angles, and bond lengths, Kuhn considered an equivalent ideal chain with N connected segments, now called Kuhn segments, that can orient in any random direction.
The length of a fully stretched chain is L = N b for the Kuhn segment chain. In the simplest treatment, such a chain follows the random walk model, where each step taken in a random direction is independent of the directions taken in the previous steps, forming a random coil. The average end-to-end distance for a chain satisfying the random walk model is ⟨ R 2 ⟩ = N b 2 .
Since the space occupied by a segment in the polymer chain cannot be taken by another segment, a self-avoiding random walk model can also be used. The Kuhn segment construction is useful in that it allows complicated polymers to be treated with simplified models as either a random walk or a self-avoiding walk, which can simplify the treatment considerably.
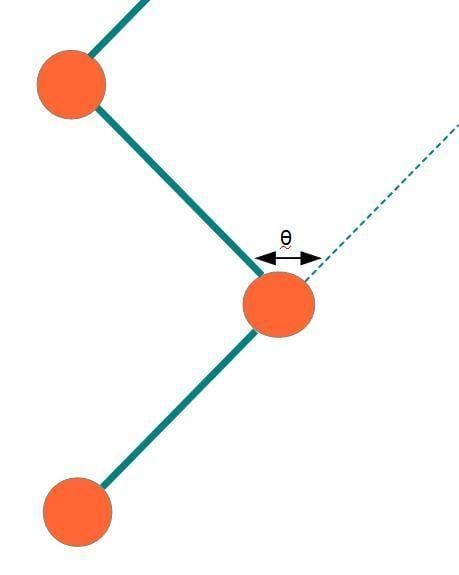
For an actual homopolymer chain (consists of the same repeat units) with bond length l and bond angle θ with a dihedral angle energy potential, the average end-to-end distance can be obtained as
⟨ R 2 ⟩ = n l 2 1 + cos ( θ ) 1 − cos ( θ ) ⋅ 1 + ⟨ cos ( ϕ ) ⟩ 1 − ⟨ cos ( ϕ ) ⟩ ,
The fully stretched length L = n l cos ( θ / 2 ) . By equating ⟨ R 2 ⟩ and L for the actual chain and the equivalent chain with Kuhn segments, the number of Kuhn segments N and the Kuhn segment length b can be obtained.
For worm-like chain, Kuhn length equals two times the persistence length.