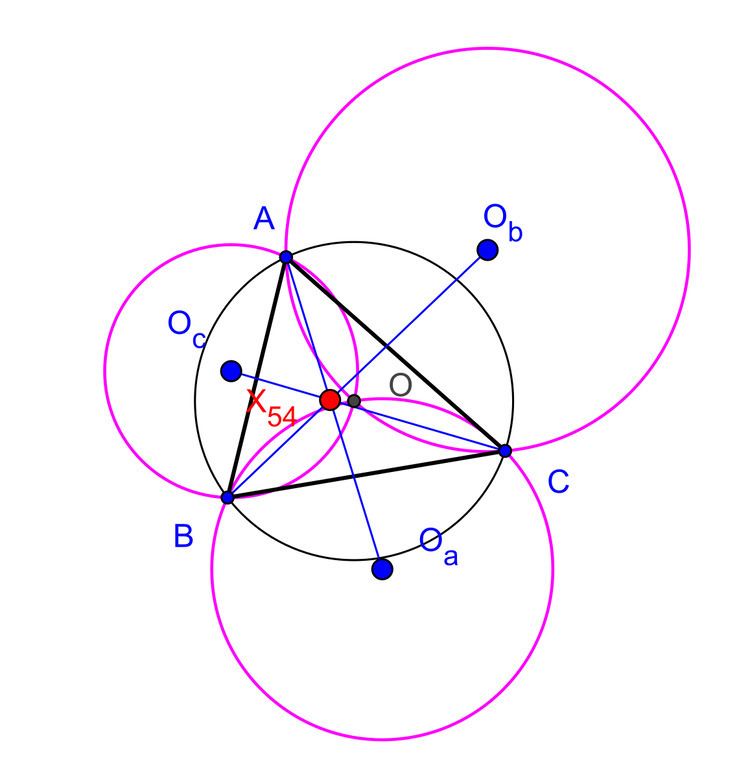
In Euclidean geometry, Kosnita's theorem is a property of certain circles associated with an arbitrary triangle.
Let A B C be an arbitrary triangle, O its circumcenter and O a , O b , O c are the circumcenters of three triangles O B C , O C A , and O A B respectively. The theorem claims that the three straight lines A O a , B O b , and C O c are concurrent. This result has been established by the Romanian mathematician Cezar Coşniţă (1910-1962).
Their point of concurrence is known as the triangle's Kosnita point (named by Rigby in 1997). It is the isogonal conjugate of the nine-point center. It is triangle center X ( 54 ) in Clark Kimberling's list. This theorem is special case of Dao's theorem on six circumcenters associated with a cyclic hexagon in.