K space (magnetic resonance imaging)

k-space is a formalism widely used in magnetic resonance imaging introduced in 1979 by Likes and in 1983 by Ljunggren and Twieg.

In MRI physics, k-space is the 2D or 3D Fourier transform of the MR image measured. Its complex values are sampled during an MR measurement, in a premeditated scheme controlled by a pulse sequence, i.e. an accurately timed sequence of radiofrequency and gradient pulses. In practice, k-space often refers to the temporary image space, usually a matrix, in which data from digitized MR signals are stored during data acquisition. When k-space is full (at the end of the scan) the data are mathematically processed to produce a final image. Thus k-space holds raw data before reconstruction.

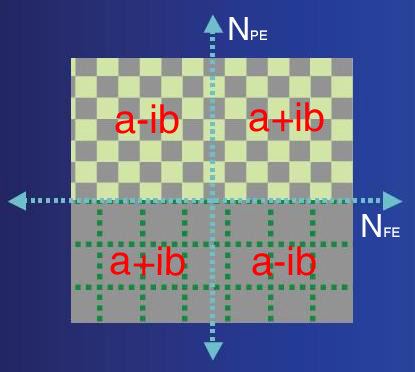
k-space is in spatial frequency domain. Thus if we define k F E and k P E such that

and

where FE refers to frequency encoding, PE to phase encoding, Δ t is the sampling time (the reciprocal of sampling frequency), τ is the duration of G_PE, γ ¯ (gamma bar) is the gyromagnetic ratio, m is the sample number in the FE direction and n is the sample number in the PE direction (also known as partition number), the 2D-Fourier Transform of this encoded signal results in a representation of the spin density distribution in two dimensions. Thus position (x,y) and spatial frequency ( k F E , k P E ) constitute a Fourier transform pair.

Typically, k-space has the same number of rows and columns as the final image and is filled with raw data during the scan, usually one line per TR (Repetition Time).

An MR image is a complex-valued map of the spatial distribution of the transverse magnetization M_xy in the sample at a specific time point after an excitation. Conventional qualitative interpretation of Fourier Analysis asserts that low spatial frequencies (near the center of k-space) contain the signal to noise and contrast information of the image, whereas high spatial frequencies (outer peripheral regions of k-space) contain the information determining the image resolution. This is the basis for advanced scanning techniques, such as the keyhole acquisition, in which a first complete k-space is acquired, and subsequent scans are performed for acquiring just the central part of the k-space; in this way, different contrast images can be acquired without the need of running full scans.

A nice symmetry property exists in k-space if the image magnetization M_xy is prepared to be proportional simply to a contrast-weighted proton density and thus is a real quantity. In such a case, the signal at two opposite locations in k-space is:

where the star ( ∗ ) denotes complex conjugation. Thus k-space information is somewhat redundant then, and an image can be reconstructed using only one half of the k-space, either in the PE (Phase Encode) direction saving scan time (such a technique is known as half Fourier or half scan) or in the FE (Frequency Encode) direction, allowing for lower sampling frequencies and/or shorter echo times (such a technique is known as half echo). However, these techniques are approximate due to phase errors in the MRI data which can rarely be completely controlled (due to imperfect static field shim, effects of spatially selective excitation, signal detection coil properties, motion etc.) or nonzero phase due to just physical reasons (such as the different chemical shift of fat and water in gradient echo techniques).