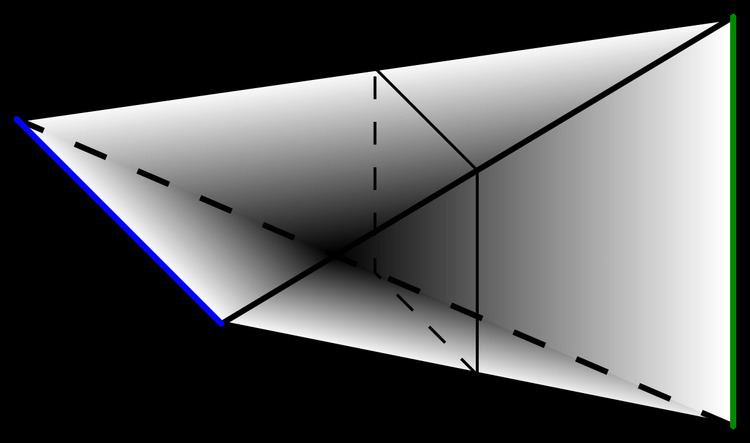
In topology, a field of mathematics, the join of two topological spaces A and B, often denoted by
A
∗
B
or
A
⋆
B
, is defined to be the quotient space
(
A
×
B
×
I
)
/
R
,
where I is the interval [0, 1] and R is the equivalence relation generated by
(
a
,
b
1
,
0
)
∼
(
a
,
b
2
,
0
)
for all
a
∈
A
and
b
1
,
b
2
∈
B
,
(
a
1
,
b
,
1
)
∼
(
a
2
,
b
,
1
)
for all
a
1
,
a
2
∈
A
and
b
∈
B
.
At the endpoints, this collapses
A
×
B
×
{
0
}
to
A
and
A
×
B
×
{
1
}
to
B
.
Intuitively,
A
⋆
B
is formed by taking the disjoint union of the two spaces and attaching a line segment joining every point in A to every point in B.
The join is homeomorphic to sum of cartesian products of cones over spaces and spaces itself, where sum is taken over cartesian product of spaces:
A
⋆
B
≅
C
(
A
)
×
B
∪
A
×
B
C
(
B
)
×
A
.
Given basepointed CW complexes (A,a0) and (B,b0), the "reduced join"
A
⋆
B
A
⋆
{
b
0
}
∪
{
a
0
}
⋆
B
is homeomorphic to the reduced suspension
Σ
(
A
∧
B
)
of the smash product. Consequently, since
A
⋆
{
b
0
}
∪
{
a
0
}
⋆
B
is contractible, there is a homotopy equivalence
A
⋆
B
≃
Σ
(
A
∧
B
)
.
The join of subsets of n-dimensional Euclidean space A and B is homotopy equivalent to the space of paths in n-dimensional Euclidean space, beginning in A and ending in B.
The join of a space X with a one-point space is called the cone CX of X.
The join of a space X with
S
0
(the 0-dimensional sphere, or, the discrete space with two points) is called the suspension
S
X
of X.
The join of the spheres
S
n
and
S
m
is the sphere
S
n
+
m
+
1
.