Jacobi's theorem (geometry)

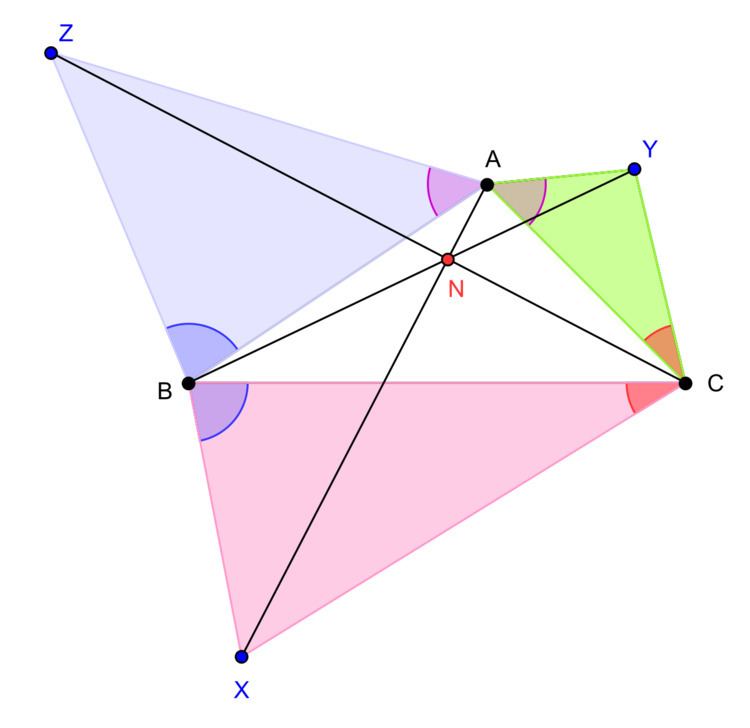
In plane geometry, a Jacobi point is a point in the Euclidean plane determined by a triangle ABC and a triple of angles α, β, and γ. This information is sufficient to determine three points X, Y, and Z such that ∠ZAB = ∠YAC = α, ∠XBC = ∠ZBA = β, and ∠YCA = ∠XCB = γ. Then, by a theorem of Karl Friedrich Andreas Jacobi, the lines AX, BY, and CZ are concurrent, at a point N called the Jacobi point.

The Jacobi point is a generalization of the Napoleon points, which are obtained by letting α = β = γ = 60°.

If the three angles above are equal, then N lies on the rectangular hyperbola given in areal coordinates by

which is Kiepert's hyperbola. Each choice of three equal angles determines a triangle center.