 | ||
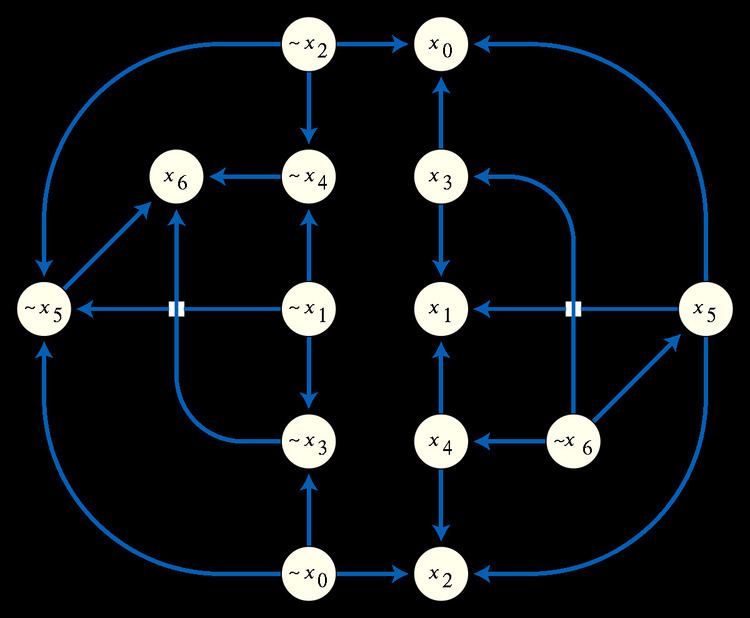
In mathematical logic, an implication graph is a skew-symmetric directed graph G(V, E) composed of vertex set V and directed edge set E. Each vertex in V represents the truth status of a Boolean literal, and each directed edge from vertex u to vertex v represents the material implication "If the literal u is true then the literal v is also true". Implication graphs were originally used for analyzing complex Boolean expressions.
Applications
A 2-satisfiability instance in conjunctive normal form can be transformed into an implication graph by replacing each of its disjunctions by a pair of implications. For example, the statement
In CDCL SAT-solvers, unit propagation can be naturally associated with an implication graph that captures all possible ways of deriving all implied literals from decision literals, which is then used for clause learning.
