Himmelblau's function

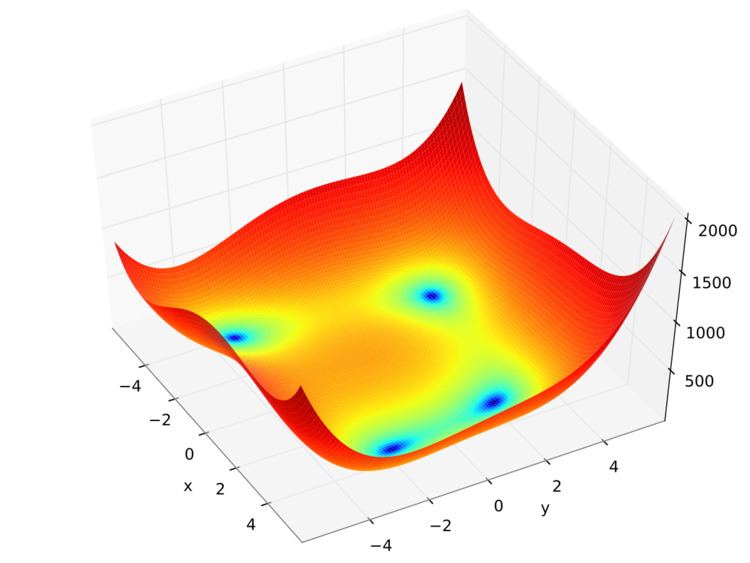
In mathematical optimization, Himmelblau's function is a multi-modal function, used to test the performance of optimization algorithms. The function is defined by:

It has one local maximum at x = − 0.270845 and y = − 0.923039 where f ( x , y ) = 181.617 , and four identical local minima:

The locations of all the minima can be found analytically. However, because they are roots of cubic polynomials, when written in terms of radicals, the expressions are somewhat complicated.

The function is named after David Mautner Himmelblau (1924–2011), who introduced it.