 | ||
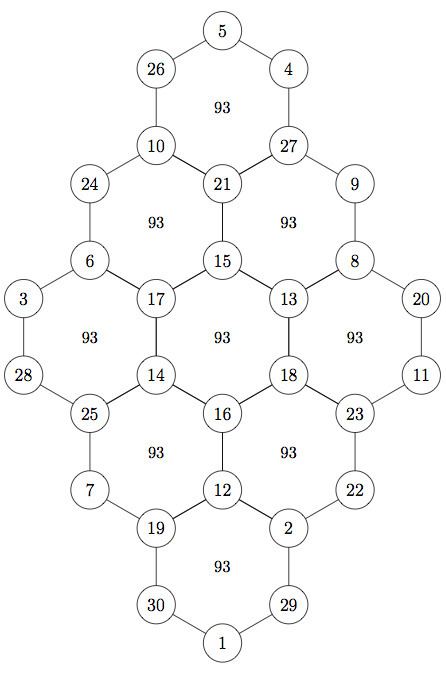
The hexagonal tortoise problem (Hangul:지수귀문도; Hanja:地數龜文圖), a.k.a. jisuguimundo, jisugwimundo) was invented by Korean aristocrat and mathematician Seok-jeong Choi, who lived from 1646 to 1715. It is a mathematical problem that involves a hexagonal lattice, like the hexagonal pattern on some tortoises' shells, to the (N) vertices of which must be assigned integers (from 1 to N) in such a way that the sum of all integers at the vertices of each hexagon is the same. The problem has apparent similarities to a magic square although it is a vertex-magic format rather than an edge-magic form or the more typical rows-of-cells form.
His book, Gu-Su-Ryak, contains many interesting mathematical discoveries. Below is his original magic hexagonal tortoise pattern. All the sums of six numbers of each hexagon are the same number, 93. The magic sum varies if the numbers 1 through 30 are rearranged. For example, the magic sum could be 77 through 109.
