Grover's algorithm - Alchetron, The Free Social Encyclopedia

Grover's algorithm is a quantum algorithm that finds with high probability the unique input to a black box function that produces a particular output value, using just O ( N ) evaluations of the function, where N is the size of the function's domain. It was devised by Lov Grover in 1996.

The analogous problem in classical computation cannot be solved in fewer than O ( N ) evaluations (because, in the worst case, the N-th member of the domain might be the correct member). At roughly the same time that Grover published his algorithm, Bennett, Bernstein, Brassard, and Vazirani proved that no quantum solution to the problem can evaluate the function fewer than O ( N ) times, so Grover's algorithm is asymptotically optimal.

Unlike other quantum algorithms, which may provide exponential speedup over their classical counterparts, Grover's algorithm provides only a quadratic speedup. However, even quadratic speedup is considerable when N is large. Grover's algorithm could brute-force a 128-bit symmetric cryptographic key in roughly 2⁶⁴ iterations, or a 256-bit key in roughly 2¹²⁸ iterations. As a result, it is sometimes suggested that symmetric key lengths be doubled to protect against future quantum attacks.

Like many quantum algorithms, Grover's algorithm is probabilistic in the sense that it gives the correct answer with a probability of less than 1. Though there is technically no upper bound on the number of repetitions that might be needed before the correct answer is obtained, the expected number of repetitions is a constant factor that does not grow with N .

Grover's original paper described the algorithm as a database search algorithm, and this description is still common. The database in this analogy is a table of all of the function's outputs, indexed by the corresponding input.

Applications

Although the purpose of Grover's algorithm is usually described as "searching a database", it may be more accurate to describe it as "inverting a function". Roughly speaking, if we have a function y = f ( x ) that can be evaluated on a quantum computer, Grover's algorithm allows us to calculate x when given y . Inverting a function is related to the searching of a database because we could come up with a function that produces one particular value of y ("true", for instance) if x matches a desired entry in a database, and another value of y ("false") for other values of x .

Grover's algorithm can also be used for estimating the mean and median of a set of numbers, and for solving the collision problem. The algorithm can be further optimized if there is more than one matching entry and the number of matches is known beforehand. Grover's algorithm can be used to crack passwords as well.

Setup

Consider an unsorted database with N entries. The algorithm requires an N-dimensional state space H, which can be supplied by n = log₂ N qubits. Consider the problem of determining the index of the database entry that satisfies some search criterion. Let f be the function that maps database entries to 0 or 1, where f(x) = 1 if and only if x satisfies the search criterion (x = ω). We are provided with (quantum black box) access to a subroutine in the form of a unitary operator U_ω that acts as follows:

{ U ω | x ⟩ = − | x ⟩ for x = ω , that is, f ( x ) = 1 , U ω | x ⟩ = | x ⟩ for x ≠ ω , that is, f ( x ) = 0.

An alternative definition of U_ω may be encountered assuming the presence of an ancillary qubit system (like in the quantum circuit depicted below). The operation then represents a conditional inversion (NOT gate) conditioned by the value of f(x) on the main system:

{ U ω | x ⟩ | y ⟩ = | x ⟩ | ¬ y ⟩ for x = ω , that is, f ( x ) = 1 , U ω | x ⟩ | y ⟩ = | x ⟩ | y ⟩ for x ≠ ω , that is, f ( x ) = 0 ,

or briefly,

U ω | x ⟩ | y ⟩ = | x ⟩ | y ⊕ f ( x ) ⟩ .

This is a natural way to realize a binary operation using the method of uncomputation. Note that if the ancillary qubit is prepared in the state | − ⟩ = 1 2 ( | 0 ⟩ − | 1 ⟩ ) = H | 1 ⟩ , the effective operation of this controlled NOT gate becomes equivalent to the original form, leaving the ancillary system disentangled from the main system:

U ω ( | x ⟩ ⊗ | − ⟩ ) = 1 2 ( U ω | x ⟩ | 0 ⟩ − U ω | x ⟩ | 1 ⟩ ) = 1 2 ( | x ⟩ | f ( x ) ⟩ − | x ⟩ | 1 ⊕ f ( x ) ⟩ ) = { 1 2 ( | x ⟩ | 1 ⟩ − | x ⟩ | 0 ⟩ ) = − | x ⟩ ⊗ | − ⟩ if f ( x ) = 1 , 1 2 ( | x ⟩ | 0 ⟩ − | x ⟩ | 1 ⟩ ) = | x ⟩ ⊗ | − ⟩ if f ( x ) = 0

In either setting, our goal is to identify the index | ω ⟩ .

Algorithm steps

The steps of Grover's algorithm are given as follows. Let | s ⟩ denote the uniform superposition over all states

| s ⟩ = 1 N ∑ x = 0 N − 1 | x ⟩ .

Then the operator

U s = 2 | s ⟩ ⟨ s | − I

is known as the Grover diffusion operator.

Here is the algorithm:

Initialize the system to the state
| s ⟩ = 1 N ∑ x = 0 N − 1 | x ⟩ .
Perform the following "Grover iteration" r(N) times. The function r(N), which is asymptotically O(N^1/2), is described below.
1. Apply the operator U ω .
2. Apply the operator U s .
Perform the measurement Ω. The measurement result will be eigenvalue λ_ω with probability approaching 1 for N ≫ 1. From λ_ω, ω may be obtained.

The first iteration

A preliminary observation, in parallel with our definition

U s = 2 | s ⟩ ⟨ s | − I ,

is that U ω can be expressed in an alternate way:

U ω = I − 2 | ω ⟩ ⟨ ω | .

To prove this it suffices to check how U ω acts on basis states:

( I − 2 | ω ⟩ ⟨ ω | ) | ω ⟩ = | ω ⟩ − 2 | ω ⟩ ⟨ ω | ω ⟩ = − | ω ⟩ = U ω | ω ⟩ , ( I − 2 | ω ⟩ ⟨ ω | ) | x ⟩ = | x ⟩ − 2 | ω ⟩ ⟨ ω | x ⟩ = | x ⟩ = U ω | x ⟩ ∀ x ≠ ω .

The following computations show what happens in the first iteration:

⟨ ω | s ⟩ = ⟨ s | ω ⟩ = 1 N , ⟨ s | s ⟩ = N 1 N ⋅ 1 N = 1 , U ω | s ⟩ = ( I − 2 | ω ⟩ ⟨ ω | ) | s ⟩ = | s ⟩ − 2 | ω ⟩ ⟨ ω | s ⟩ = | s ⟩ − 2 N | ω ⟩ , U s ( | s ⟩ − 2 N | ω ⟩ ) = ( 2 | s ⟩ ⟨ s | − I ) ( | s ⟩ − 2 N | ω ⟩ ) = 2 | s ⟩ ⟨ s | s ⟩ − | s ⟩ − 4 N | s ⟩ ⟨ s | ω ⟩ + 2 N | ω ⟩ = 2 | s ⟩ − | s ⟩ − 4 N ⋅ 1 N | s ⟩ + 2 N | ω ⟩ = | s ⟩ − 4 N | s ⟩ + 2 N | ω ⟩ = N − 4 N | s ⟩ + 2 N | ω ⟩ .

It is worth noting the special case of N = 4 with a single marked state. This has U s U w | s ⟩ = | ω ⟩ , meaning that in a single application of the Grover iterator the marked state is returned.

After application of the operators U ω and U s , the square amplitude of the queried element has increased from | ⟨ ω | s ⟩ | 2 = 1 N to | ⟨ ω | U s U ω | s ⟩ | 2 = ( 3 N − 4 ) 2 N 3 .

Description of Uω

Grover's algorithm requires a "quantum oracle" operator U ω , which can recognize solutions to the search problem and give them a negative sign. In order to keep the search algorithm general, we will leave the inner workings of the oracle as a black box, but will explain how the sign is flipped. The oracle contains a function f that returns f ( x ) = 1 if | x ⟩ is a solution to the search problem and f ( x ) = 0 otherwise. The oracle is a unitary operator operating on two qubits:

| x ⟩ | q ⟩ ⟶ U ω | x ⟩ | q ⊕ f ( x ) ⟩ ,

where | x ⟩ is the index qubit and | q ⟩ is the oracle qubit.

As usual, ⊕ denotes addition modulo 2. The operation flips the oracle qubit if f ( x ) = 1 and leaves it unchanged otherwise. In Grover's algorithm we want to flip the sign of the state | x ⟩ if it labels a solution. This is achieved by setting the oracle qubit in the state ( | 0 ⟩ − | 1 ⟩ ) / 2 , which is flipped to ( | 1 ⟩ − | 0 ⟩ ) / 2 if | x ⟩ is a solution:

| x ⟩ ( | 0 ⟩ − | 1 ⟩ ) / 2 ⟶ U ω ( − 1 ) f ( x ) | x ⟩ ( | 0 ⟩ − | 1 ⟩ ) / 2 .

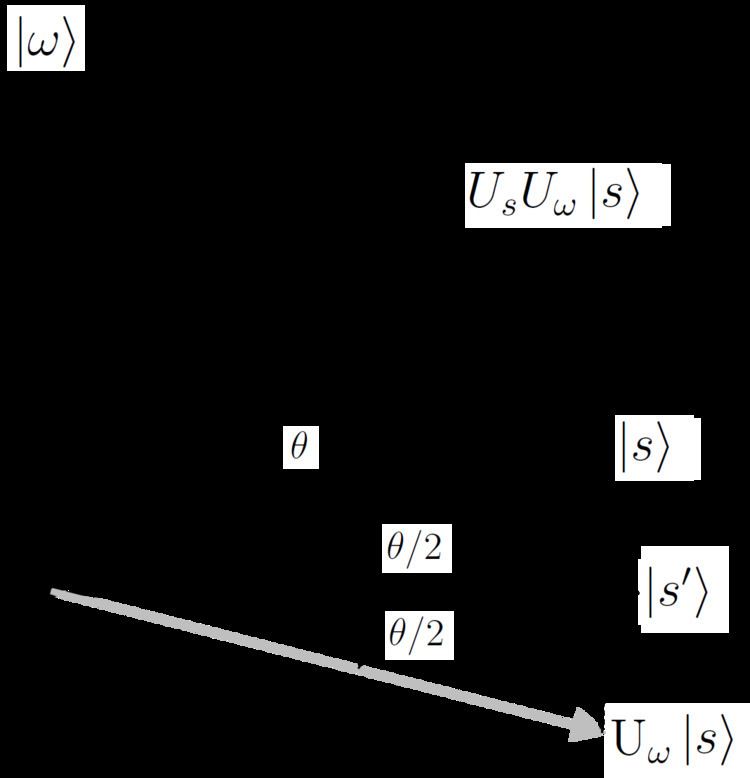
We regard | x ⟩ as flipped, thus the oracle qubit is not changed, so by convention the oracle qubits are usually not mentioned in the specification of Grover's algorithm. Thus the operation of the oracle U ω is simply written as

| x ⟩ ⟶ U ω ( − 1 ) f ( x ) | x ⟩ .

Geometric proof of correctness

⟨ s ′ | s ⟩ = N − 1 N .

In geometric terms, the angle θ / 2 between | s ⟩ and | s ′ ⟩ is given by

sin ⁡ θ 2 = 1 N .

The operator U ω is a reflection at the hyperplane orthogonal to | ω ⟩ for vectors in the plane spanned by | s ′ ⟩ and | ω ⟩ , i.e. it acts as a reflection across | s ′ ⟩ . The operator U s is a reflection through | s ⟩ . Therefore, the state vector remains in the plane spanned by | s ′ ⟩ and | ω ⟩ after each application of the operators U s and U ω , and it is straightforward to check that the operator U s U ω of each Grover iteration step rotates the state vector by an angle of θ = 2 arcsin ⁡ 1 N .

We need to stop when the state vector passes close to | ω ⟩ ; after this, subsequent iterations rotate the state vector away from | ω ⟩ , reducing the probability of obtaining the correct answer. The exact probability of measuring the correct answer is

sin 2 ⁡ ( ( r + 1 2 ) θ ) ,

where r is the (integer) number of Grover iterations. The earliest time that we get a near-optimal measurement is therefore r ≈ π N / 4 .

Algebraic proof of correctness

To complete the algebraic analysis, we need to find out what happens when we repeatedly apply U s U ω . A natural way to do this is by eigenvalue analysis of a matrix. Notice that during the entire computation, the state of the algorithm is a linear combination of s and ω . We can write the action of U s and U ω in the space spanned by { | s ⟩ , | ω ⟩ } as:

U s : a | ω ⟩ + b | s ⟩ ↦ ( | ω ⟩ | s ⟩ ) ( − 1 0 2 / N 1 ) ( a b ) . U ω : a | ω ⟩ + b | s ⟩ ↦ ( | ω ⟩ | s ⟩ ) ( − 1 − 2 / N 0 1 ) ( a b ) .

So in the basis { | ω ⟩ , | s ⟩ } (which is neither orthogonal nor a basis of the whole space) the action U s U ω of applying U ω followed by U s is given by the matrix

U s U ω = ( − 1 0 2 / N 1 ) ( − 1 − 2 / N 0 1 ) = ( 1 2 / N − 2 / N 1 − 4 / N ) .

This matrix happens to have a very convenient Jordan form. If we define t = arcsin ⁡ ( 1 / N ) , it is

U s U ω = M ( exp ⁡ ( 2 i t ) 0 0 exp ⁡ ( − 2 i t ) ) M − 1 where M = ( − i i exp ⁡ ( i t ) exp ⁡ ( − i t ) ) .

It follows that r-th power of the matrix (corresponding to r iterations) is

( U s U ω ) r = M ( exp ⁡ ( 2 r i t ) 0 0 exp ⁡ ( − 2 r i t ) ) M − 1 .

Using this form, we can use trigonometric identities to compute the probability of observing ω after r iterations mentioned in the previous section,

| ( ⟨ ω | ω ⟩ ⟨ ω | s ⟩ ) ( U s U ω ) r ( 0 1 ) | 2 = sin 2 ⁡ ( ( 2 r + 1 ) t ) .

Alternatively, one might reasonably imagine that a near-optimal time to distinguish would be when the angles 2rt and −2rt are as far apart as possible, which corresponds to 2 r t ≈ π / 2 , or r = π / 4 t = π / 4 arcsin ⁡ ( 1 / N ) ≈ π N / 4 . Then the system is in state

( | ω ⟩ | s ⟩ ) ( U s U ω ) r ( 0 1 ) ≈ ( | ω ⟩ | s ⟩ ) M ( i 0 0 − i ) M − 1 ( 0 1 ) = | ω ⟩ 1 cos ⁡ ( t ) − | s ⟩ sin ⁡ ( t ) cos ⁡ ( t ) .

A short calculation now shows that the observation yields the correct answer ω with error O(1/N).

Extension to space with multiple targets

If, instead of 1 matching entry, there are k matching entries, the same algorithm works, but the number of iterations must be π(N/k)^1/2/4 instead of πN^1/2/4. There are several ways to handle the case if k is unknown. For example, one could run Grover's algorithm several times, with

π N 1 / 2 4 , π ( N / 2 ) 1 / 2 4 , π ( N / 4 ) 1 / 2 4 , …

iterations. For any k, one of the iterations will find a matching entry with a sufficiently high probability. The total number of iterations is at most

π N 1 / 2 4 ( 1 + 1 2 + 1 2 + ⋯ ) = π N 1 / 2 4 ( 2 + 2 ) ,

which is still O(N^1/2). It can be shown that this can be improved. If the number of marked items is k, where k is unknown, there is an algorithm that finds the solution in N / k queries. This fact is used in order to solve the collision problem.

Quantum partial search

A modification of Grover's algorithm called quantum partial search was described by Grover and Radhakrishnan in 2004. In partial search, one is not interested in finding the exact address of the target item, only the first few digits of the address. Equivalently, we can think of "chunking" the search space into blocks, and then asking "in which block is the target item?". In many applications, such a search yields enough information if the target address contains the information wanted. For instance, to use the example given by L. K. Grover, if one has a list of students organized by class rank, we may only be interested in whether a student is in the lower 25%, 25–50%, 50–75% or 75–100% percentile.

To describe partial search, we consider a database separated into K blocks, each of size b = N / K . Obviously, the partial search problem is easier. Consider the approach we would take classically – we pick one block at random, and then perform a normal search through the rest of the blocks (in set theory language, the complement). If we don't find the target, then we know it's in the block we didn't search. The average number of iterations drops from N / 2 to ( N − b ) / 2 .

Grover's algorithm requires π / 4 N iterations. Partial search will be faster by a numerical factor that depends on the number of blocks K . Partial search uses n 1 global iterations and n 2 local iterations. The global Grover operator is designated G 1 and the local Grover operator is designated G 2 .

The global Grover operator acts on the blocks. Essentially, it is given as follows:

Perform j 1 standard Grover iterations on the entire database.
Perform j 2 local Grover iterations. A local Grover iteration is a direct sum of Grover iterations over each block.
Perform one standard Grover iteration.

The optimal values of j 1 and j 2 are discussed in the paper by Grover and Radhakrishnan. One might also wonder what happens if one applies successive partial searches at different levels of "resolution". This idea was studied in detail by Korepin and Xu, who called it binary quantum search. They proved that it is not in fact any faster than performing a single partial search.

Optimality

It is known that Grover's algorithm is optimal. That is, any algorithm that accesses the database only by using the operator U_ω must apply U_ω at least as many times as Grover's algorithm. This result is important in understanding the limits of quantum computation.

If the Grover's search problem was solvable with log^c N applications of U_ω, that would imply that NP is contained in BQP, by transforming problems in NP into Grover-type search problems. The optimality of Grover's algorithm suggests (but does not prove) that NP is not contained in BQP.

The number of iterations for k matching entries, π(N/k)^1/2/4, is also optimal.

Applicability and limitations

When applications of Grover's algorithm are considered, it should be emphasized that the database is not represented explicitly. Instead, an oracle is invoked to evaluate an item by its index. Reading a full data-base item by item and converting it into such a representation may take a lot longer than Grover's search. To account for such effects, Grover's algorithm can be viewed as solving an equation or satisfying a constraint. In such applications, the oracle is a way to check the constraint and is not related to the search algorithm. This separation usually prevents algorithmic optimizations, whereas conventional search algorithms often rely on such optimizations and avoid exhaustive search. These and other considerations about using Grover's algorithm are discussed in a paper by Viamontes, Markov and Hayes.

References

Grover's algorithm Wikipedia

(Text) CC BY-SA

Contents