 | ||
In computer science theory – particularly formal language theory – the Glushkov Construction Algorithm (GCA) transforms a given regular expression into an equivalent nondeterministic finite automaton (NFA). Thus, it forms a bridge between regular expressions and nondeterministic finite automata: two abstract representations of formal languages.
Contents
- Construction
- Example
- Computation of the set of letters
- Properties
- Applications and deterministic expressions
- References
The NFA format is better suited for execution on a computer when regular expressions are used. These expressions may be used to describe advanced search patterns in "find and replace"-like operations of text processing utilities. This algorithm can be considered a compiler from a regular expression to an NFA, which is why this algorithm is of practical interest. Furthermore, the automaton is small by nature, as the number of states is equal to the number of letters of the regular expression, plus one.
Thus, an automaton can be made deterministic by the powerset construction and then be minimized to get an optimal automaton corresponding to the given regular expression.
From another, more theoretical point of view, this algorithm is a part of the proof that they both accept exactly the same languages; that is, the regular languages. The converse of Glushkov's algorithm is Kleene's algorithm, which transforms a finite automaton into a regular expression. The automaton obtained by Glushkov's construction is the same as the one obtained by Thompson's construction algorithm, once their ε-transition is removed.
Construction
Given a regular expression
1. Linearisation of the expression. Each letter of the alphabet appearing in the expression is renamed, so that each letter occurs at most once in the new expression. Let
2a. Computation of the sets
They are computed by induction over the structure of the expression, as explained below, but they are a function of the language and not of the expression.
2b. Computation of the set
3. Computation of the local language, as defined by
potentially with the empty word.
The computation of the automaton for the local language denoted by this linearised expression is formally known as Glushkov's construction. The construction of the automaton can be done using classical construction operations: concatenation, intersection and itering an automaton.
4. Erasing the delineation, giving to each letter of
Example
Consider the rational expression
1. The linearized version is
The letters have been linearized by appending an index to them.
2. The sets
The empty word belongs to the language, hence
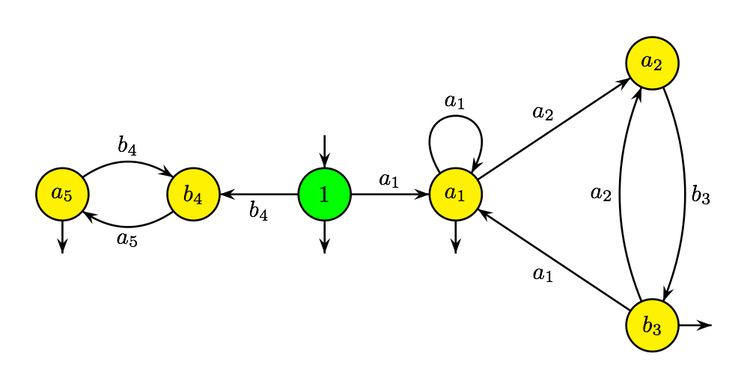
3. The automaton of the local language
contains an initial state, denoted 1, and a state for each of the five letters of the alphabet
There is a transition from 1 to the two states of
4. Obtain the automaton for
Computation of the set of letters
The computation of the sets
1. For
for all letters
and then
2. For
for each letter
and finally
The same formulas are also correct for
3. For the set of factors of length 2, one has
for all letters
and finally
The most costly operations are the products of sets for the computation of
Properties
The obtained automaton is non-deterministic, and it has as many states as the number of letters of the rational expression, plus one. Furthermore, it has been shown that Glushkov's automaton is the same as Thompson's automaton when the ε-transitions are removed.
Applications and deterministic expressions
The computation of the automaton by the expression occurs often; it has been systematically used in search functions, in particular by the Unix grep command. Similarly, XML's specification also uses such constructions; for more efficiency, regular expressions of a certain kind, called deterministic expressions, have been studied.
