Gires–Tournois etalon - Alchetron, The Free Social Encyclopedia

In optics, a Gires–Tournois etalon is a transparent plate with two reflecting surfaces, one of which has very high reflectivity. Due to multiple-beam interference, light incident on a Gires–Tournois etalon is (almost) completely reflected, but has an effective phase shift that depends strongly on the wavelength of the light.

The complex amplitude reflectivity of a Gires–Tournois etalon is given by

r = − r 1 − e − i δ 1 − r 1 e − i δ

where r₁ is the complex amplitude reflectivity of the first surface,

δ = 4 π λ n t cos ⁡ θ t n is the index of refraction of the plate t is the thickness of the plate θ_t is the angle of refraction the light makes within the plate, and λ is the wavelength of the light in vacuum.

Nonlinear effective phase shift

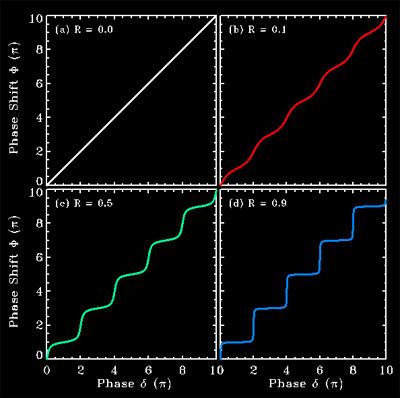
Suppose that r 1 is real. Then | r | = 1 , independent of δ . This indicates that all the incident energy is reflected and intensity is uniform. However, the multiple reflection causes a nonlinear phase shift Φ .

To show this effect, we assume r 1 is real and r 1 = R , where R is the intensity reflectivity of the first surface. Define the effective phase shift Φ through

r = e i Φ .

One obtains

tan ⁡ ( Φ 2 ) = − 1 + R 1 − R tan ⁡ ( δ 2 )

For R = 0, no reflection from the first surface and the resultant nonlinear phase shift is equal to the round-trip phase change ( Φ = δ ) – linear response. However, as can be seen, when R is increased, the nonlinear phase shift Φ gives the nonlinear response to δ and shows step-like behavior. Gires–Tournois etalon has applications for laser pulse compression and nonlinear Michelson interferometer.

Gires–Tournois etalons are closely related to Fabry–Pérot etalons.

References

Gires–Tournois etalon Wikipedia

(Text) CC BY-SA