Supriya Ghosh (Editor)

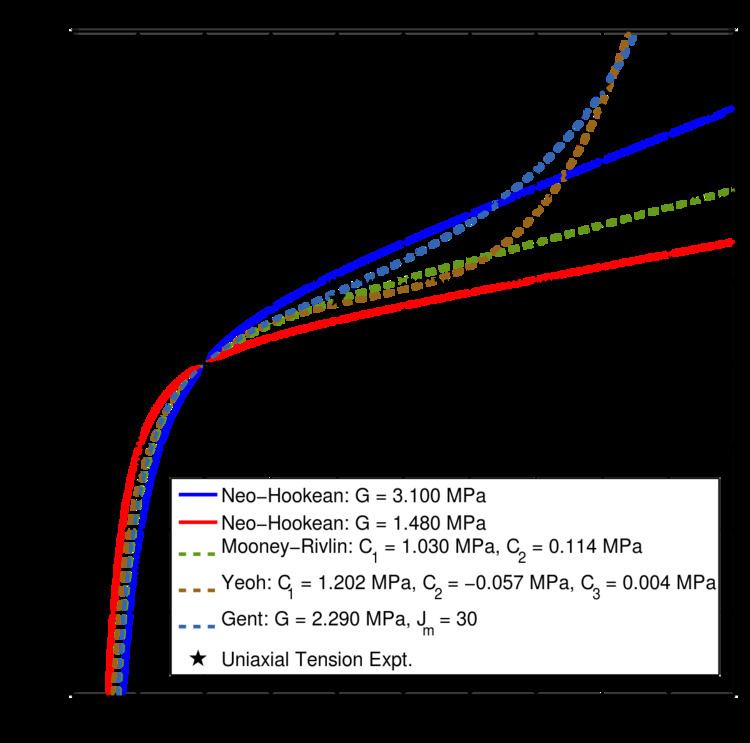
Gent (hyperelastic model)

Updated on
Edit
Like
Comment
Share on FacebookTweet on TwitterShare on LinkedInShare on Reddit
Gent (hyperelastic model)

The Gent hyperelastic material model is a phenomenological model of rubber elasticity that is based on the concept of limiting chain extensibility. In this model, the strain energy density function is designed such that it has a singularity when the first invariant of the left Cauchy-Green deformation tensor reaches a limiting value I m .

Contents

The strain energy density function for the Gent model is

W = − μ J m 2 ln ⁡ ( 1 − I 1 − 3 J m )

where μ is the shear modulus and J m = I m − 3 .

In the limit where I m → ∞ , the Gent model reduces to the Neo-Hookean solid model. This can be seen by expressing the Gent model in the form

W = − μ 2 x ln ⁡ [ 1 − ( I 1 − 3 ) x ]   ;     x := 1 J m

A Taylor series expansion of ln ⁡ [ 1 − ( I 1 − 3 ) x ] around x = 0 and taking the limit as x → 0 leads to

W = μ 2 ( I 1 − 3 )

which is the expression for the strain energy density of a Neo-Hookean solid.

Several compressible versions of the Gent model have been designed. One such model has the form

W = − μ J m 2 ln ⁡ ( 1 − I 1 − 3 J m ) + κ 2 ( J 2 − 1 2 − ln ⁡ J ) 4

where J = det ( F ) , κ is the bulk modulus, and F is the deformation gradient.

Consistency condition

We may alternatively express the Gent model in the form

W = C 0 ln ⁡ ( 1 − I 1 − 3 J m )

For the model to be consistent with linear elasticity, the following condition has to be satisfied:

2 ∂ W ∂ I 1 ( 3 ) = μ

where μ is the shear modulus of the material. Now, at I 1 = 3 ( λ i = λ j = 1 ) ,

∂ W ∂ I 1 = − C 0 J m

Therefore, the consistency condition for the Gent model is

− 2 C 0 J m = μ ⟹ C 0 = − μ J m 2

The Gent model assumes that J m ≫ 1

Stress-deformation relations

The Cauchy stress for the incompressible Gent model is given by

σ = − p   1 + 2   ∂ W ∂ I 1   B = − p   1 + μ J m J m − I 1 + 3   B

Uniaxial extension

For uniaxial extension in the n 1 -direction, the principal stretches are λ 1 = λ ,   λ 2 = λ 3 . From incompressibility λ 1   λ 2   λ 3 = 1 . Hence λ 2 2 = λ 3 2 = 1 / λ . Therefore,

I 1 = λ 1 2 + λ 2 2 + λ 3 2 = λ 2 + 2 λ   .

The left Cauchy-Green deformation tensor can then be expressed as

B = λ 2   n 1 ⊗ n 1 + 1 λ   ( n 2 ⊗ n 2 + n 3 ⊗ n 3 )   .

If the directions of the principal stretches are oriented with the coordinate basis vectors, we have

σ 11 = − p + λ 2 μ J m J m − I 1 + 3   ;     σ 22 = − p + μ J m λ ( J m − I 1 + 3 ) = σ 33   .

If σ 22 = σ 33 = 0 , we have

p = μ J m λ ( J m − I 1 + 3 )   .

Therefore,

σ 11 = ( λ 2 − 1 λ ) ( μ J m J m − I 1 + 3 )   .

The engineering strain is λ − 1 . The engineering stress is

T 11 = σ 11 / λ = ( λ − 1 λ 2 ) ( μ J m J m − I 1 + 3 )   .

Equibiaxial extension

For equibiaxial extension in the n 1 and n 2 directions, the principal stretches are λ 1 = λ 2 = λ . From incompressibility λ 1   λ 2   λ 3 = 1 . Hence λ 3 = 1 / λ 2 . Therefore,

I 1 = λ 1 2 + λ 2 2 + λ 3 2 = 2   λ 2 + 1 λ 4   .

The left Cauchy-Green deformation tensor can then be expressed as

B = λ 2   n 1 ⊗ n 1 + λ 2   n 2 ⊗ n 2 + 1 λ 4   n 3 ⊗ n 3   .

If the directions of the principal stretches are oriented with the coordinate basis vectors, we have

σ 11 = ( λ 2 − 1 λ 4 ) ( μ J m J m − I 1 + 3 ) = σ 22   .

The engineering strain is λ − 1 . The engineering stress is

T 11 = σ 11 λ = ( λ − 1 λ 5 ) ( μ J m J m − I 1 + 3 ) = T 22   .

Planar extension

Planar extension tests are carried out on thin specimens which are constrained from deforming in one direction. For planar extension in the n 1 directions with the n 3 direction constrained, the principal stretches are λ 1 = λ ,   λ 3 = 1 . From incompressibility λ 1   λ 2   λ 3 = 1 . Hence λ 2 = 1 / λ . Therefore,

I 1 = λ 1 2 + λ 2 2 + λ 3 2 = λ 2 + 1 λ 2 + 1   .

The left Cauchy-Green deformation tensor can then be expressed as

B = λ 2   n 1 ⊗ n 1 + 1 λ 2   n 2 ⊗ n 2 + n 3 ⊗ n 3   .

If the directions of the principal stretches are oriented with the coordinate basis vectors, we have

σ 11 = ( λ 2 − 1 λ 2 ) ( μ J m J m − I 1 + 3 )   ;     σ 22 = 0   ;     σ 33 = ( 1 − 1 λ 2 ) ( μ J m J m − I 1 + 3 )   .

The engineering strain is λ − 1 . The engineering stress is

T 11 = σ 11 λ = ( λ − 1 λ 3 ) ( μ J m J m − I 1 + 3 )   .

Simple shear

The deformation gradient for a simple shear deformation has the form

F = 1 + γ   e 1 ⊗ e 2

where e 1 , e 2 are reference orthonormal basis vectors in the plane of deformation and the shear deformation is given by

γ = λ − 1 λ   ;     λ 1 = λ   ;     λ 2 = 1 λ   ;     λ 3 = 1

In matrix form, the deformation gradient and the left Cauchy-Green deformation tensor may then be expressed as

F = [ 1 γ 0 0 1 0 0 0 1 ]   ;     B = F ⋅ F T = [ 1 + γ 2 γ 0 γ 1 0 0 0 1 ]

Therefore,

I 1 = t r ( B ) = 3 + γ 2

and the Cauchy stress is given by

σ = − p   1 + μ J m J m − γ 2   B

In matrix form,

σ = [ − p + μ J m ( 1 + γ 2 ) J m − γ 2 μ J m γ J m − γ 2 0 μ J m γ J m − γ 2 − p + μ J m J m − γ 2 0 0 0 − p + μ J m J m − γ 2 ]

References

Gent (hyperelastic model) Wikipedia
(Text) CC BY-SA


Similar Topics