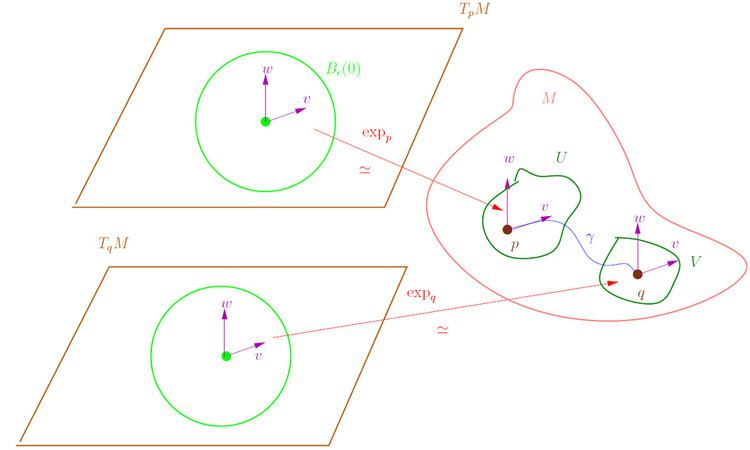
In Riemannian geometry, Gauss's lemma asserts that any sufficiently small sphere centered at a point in a Riemannian manifold is perpendicular to every geodesic through the point. More formally, let M be a Riemannian manifold, equipped with its Levi-Civita connection, and p a point of M. The exponential map is a mapping from the tangent space at p to M:
e x p : T p M → M which is a diffeomorphism in a neighborhood of zero. Gauss' lemma asserts that the image of a sphere of sufficiently small radius in TpM under the exponential map is perpendicular to all geodesics originating at p. The lemma allows the exponential map to be understood as a radial isometry, and is of fundamental importance in the study of geodesic convexity and normal coordinates.
We define the exponential map at p ∈ M by
exp p : T p M ⊃ B ϵ ( 0 ) ⟶ M , v ⟼ γ p , v ( 1 ) , where γ p , v is the unique geodesic with γ ( 0 ) = p and tangent γ p , v ′ ( 0 ) = v ∈ T p M and ϵ 0 is chosen small enough so that for every v ∈ B ϵ ( 0 ) ⊂ T p M the geodesic γ p , v is defined in 1. So, if M is complete, then, by the Hopf–Rinow theorem, exp p is defined on the whole tangent space.
Let α : I → T p M be a curve differentiable in T p M such that α ( 0 ) := 0 and α ′ ( 0 ) := v . Since T p M ≅ R n , it is clear that we can choose α ( t ) := v t . In this case, by the definition of the differential of the exponential in 0 applied over v , we obtain:
T 0 exp p ( v ) = d d t ( exp p ∘ α ( t ) ) | t = 0 = d d t ( exp p ( v t ) ) | t = 0 = d d t ( γ ( 1 , p , v t ) ) | t = 0 = γ ′ ( t , p , v ) | t = 0 = v . So (with the right identification T 0 T p M ≅ T p M ) the differential of exp p is the identity. By the implicit function theorem, exp p is a diffeomorphism on a neighborhood of 0 ∈ T p M . The Gauss Lemma now tells that exp p is also a radial isometry.
Let p ∈ M . In what follows, we make the identification T v T p M ≅ T p M ≅ R n .
Gauss's Lemma states: Let v , w ∈ B ϵ ( 0 ) ⊂ T v T p M ≅ T p M and M ∋ q := exp p ( v ) . Then, ⟨ T v exp p ( v ) , T v exp p ( w ) ⟩ q = ⟨ v , w ⟩ p .
For p ∈ M , this lemma means that exp p is a radial isometry in the following sense: let v ∈ B ϵ ( 0 ) , i.e. such that exp p is well defined. And let q := exp p ( v ) ∈ M . Then the exponential exp p remains an isometry in q , and, more generally, all along the geodesic γ (in so far as γ ( 1 , p , v ) = exp p ( v ) is well defined)! Then, radially, in all the directions permitted by the domain of definition of exp p , it remains an isometry.
Recall that
T v exp p : T p M ≅ T v T p M ⊃ T v B ϵ ( 0 ) ⟶ T exp p ( v ) M .
We proceed in three steps:
T v exp p ( v ) = v : let us construct a curve α : R ⊃ I → T p M such that α ( 0 ) := v ∈ T p M and α ′ ( 0 ) := v ∈ T v T p M ≅ T p M . Since T v T p M ≅ T p M ≅ R n , we can put α ( t ) := v ( t + 1 ) . We find that, thanks to the identification we have made, and since we are only taking equivalence classes of curves, it is possible to choose α ( t ) = v t (these are exactly the same curves, but shifted because of the domain of definition I ; however, the identification allows us to gather them around 0 . Hence,
T v exp p ( v ) = d d t ( exp p ∘ α ( t ) ) | t = 0 = d d t γ ( t , p , v ) | t = 0 = v . Now let us calculate the scalar product ⟨ T v exp p ( v ) , T v exp p ( w ) ⟩ .
We separate w into a component w T parallel to v and a component w N normal to v . In particular, we put w T := a v , a ∈ R .
The preceding step implies directly:
⟨ T v exp p ( v ) , T v exp p ( w ) ⟩ = ⟨ T v exp p ( v ) , T v exp p ( w T ) ⟩ + ⟨ T v exp p ( v ) , T v exp p ( w N ) ⟩ We must therefore show that the second term is null, because, according to Gauss's Lemma, we must have:
⟨ T v exp p ( v ) , T v exp p ( w N ) ⟩ = ⟨ v , w N ⟩ = 0.
⟨ T v exp p ( v ) , T v exp p ( w N ) ⟩ = 0 :Let us define the curve
α : [ − ϵ , ϵ ] × [ 0 , 1 ] ⟶ T p M , ( s , t ) ⟼ t v + t s w N . Note that
α ( 0 , 1 ) = v , ∂ α ∂ t ( s , t ) = v + s w N , ∂ α ∂ s ( 0 , t ) = t w N . Let us put:
f : [ − ϵ , ϵ ] × [ 0 , 1 ] ⟶ M , ( s , t ) ⟼ exp p ( t v + t s w N ) , and we calculate:
T v exp p ( v ) = T α ( 0 , 1 ) exp p ( ∂ α ∂ t ( 0 , 1 ) ) = ∂ ∂ t ( exp p ∘ α ( s , t ) ) | t = 1 , s = 0 = ∂ f ∂ t ( 0 , 1 ) and
T v exp p ( w N ) = T α ( 0 , 1 ) exp p ( ∂ α ∂ s ( 0 , 1 ) ) = ∂ ∂ s ( exp p ∘ α ( s , t ) ) | t = 1 , s = 0 = ∂ f ∂ s ( 0 , 1 ) . Hence
⟨ T v exp p ( v ) , T v exp p ( w N ) ⟩ = ⟨ ∂ f ∂ t , ∂ f ∂ s ⟩ ( 0 , 1 ) . We can now verify that this scalar product is actually independent of the variable t , and therefore that, for example:
⟨ ∂ f ∂ t , ∂ f ∂ s ⟩ ( 0 , 1 ) = ⟨ ∂ f ∂ t , ∂ f ∂ s ⟩ ( 0 , 0 ) = 0 , because, according to what has been given above:
lim t → 0 ∂ f ∂ s ( 0 , t ) = lim t → 0 T t v exp p ( t w N ) = 0 being given that the differential is a linear map. This will therefore prove the lemma.
We verify that ∂ ∂ t ⟨ ∂ f ∂ t , ∂ f ∂ s ⟩ = 0 : this is a direct calculation. Since the maps t ↦ f ( s , t ) are geodesics, ∂ ∂ t ⟨ ∂ f ∂ t , ∂ f ∂ s ⟩ = ⟨ D ∂ t ∂ f ∂ t ⏟ = 0 , ∂ f ∂ s ⟩ + ⟨ ∂ f ∂ t , D ∂ t ∂ f ∂ s ⟩ = ⟨ ∂ f ∂ t , D ∂ s ∂ f ∂ t ⟩ = 1 2 ∂ ∂ s ⟨ ∂ f ∂ t , ∂ f ∂ t ⟩ . Since the maps t ↦ f ( s , t ) are geodesics, the function t ↦ ⟨ ∂ f ∂ t , ∂ f ∂ t ⟩ is constant. Thus,
∂ ∂ s ⟨ ∂ f ∂ t , ∂ f ∂ t ⟩ = ∂ ∂ s ⟨ v + s w N , v + s w N ⟩ = 2 ⟨ v , w N ⟩ = 0.