Fundamental theorem of linear algebra

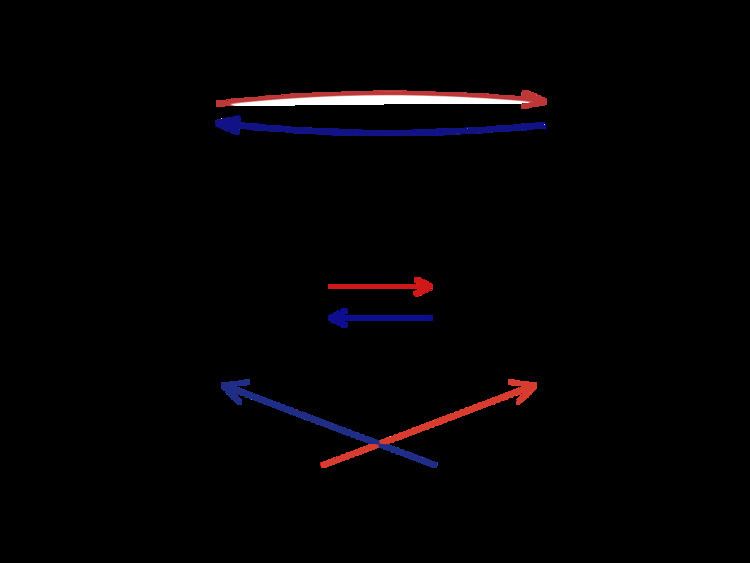
In mathematics, the fundamental theorem of linear algebra makes several statements regarding vector spaces. These may be stated concretely in terms of the rank r of an m × n matrix A and its singular value decomposition:

First, each matrix A ∈ R m × n ( A has m rows and n columns) induces four fundamental subspaces. These fundamental subspaces are:

Secondly:

1. In R n , ker ⁡ ( A ) = ( im ⁡ ( A T ) ) ⊥ , that is, the nullspace is the orthogonal complement of the row space
2. In R m , ker ⁡ ( A T ) = ( im ⁡ ( A ) ) ⊥ , that is, the left nullspace is the orthogonal complement of the column space.

The dimensions of the subspaces are related by the rank–nullity theorem, and follow from the above theorem.

Further, all these spaces are intrinsically defined—they do not require a choice of basis—in which case one rewrites this in terms of abstract vector spaces, operators, and the dual spaces as A : V → W and A ∗ : W ∗ → V ∗ : the kernel and image of A ∗ are the cokernel and coimage of A .