In number theory, Firoozbakht’s conjecture (or the Firoozbakht conjecture) is a conjecture about the distribution of prime numbers. It is named after the Iranian mathematician Farideh Firoozbakht from the University of Isfahan who stated it first in 1982.
The conjecture states that p n 1 / n (where p n is the nth prime) is a strictly decreasing function of n, i.e.,
p n + 1 1 / ( n + 1 ) < p n 1 / n for all n ≥ 1. Equivalently: p n + 1 < p n 1 + 1 n for all n ≥ 1 , see A182134, A246782.
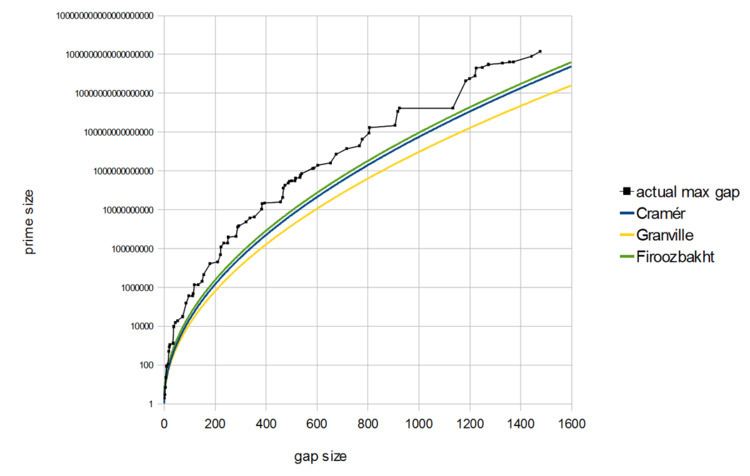
By using a table of maximal gaps, Farideh Firoozbakht verified her conjecture up to 4.444×1012. Now with more extensive tables of maximal gaps, the conjecture has been verified for all primes below 4×1018.
If the conjecture were true, then the prime gap function g n = p n + 1 − p n would satisfy g n < ( log p n ) 2 − log p n for all n > 4 and, moreover, g n < ( log p n ) 2 − log p n − 1 for all n > 9 ; see also A111943. This is among the strongest upper bounds conjectured for prime gaps, even somewhat stronger than the Cramér and Shanks conjectures. It implies a strong form of Cramér's conjecture and is hence is inconsistent with the heuristics of Granville and Pintz and of Maier which suggest that g n > 2 − ε e γ ( log p n ) 2 infinitely often for any ε > 0 , where γ denotes the Euler–Mascheroni constant.
Two related conjectures (see the comments of A182514) are
( log ( p n + 1 ) log ( p n ) ) n < e ,
which is weaker, and
( p n + 1 p n ) n < n log ( n ) for all values with
n > 5 ,
which is stronger.