 | ||
Similar Euclid books, Other books | ||
Euclid's Optics (Greek: Ὀπτικά), is a work on the geometry of vision written by the Greek mathematician Euclid around 300 BC. The earliest surviving manuscript of Optics is in Greek and dates from the 10th century AD.
Contents
The work deals almost entirely with the geometry of vision, with little reference to either the physical or psychological aspects of sight. No Western scientist had previously given such mathematical attention to vision. Euclid's Optics influenced the work of later Greek, Islamic, and Western European Renaissance scientists and artists.
Historical significance
Writers before Euclid had developed theories of vision. However, their works were mostly philosophical in nature and lacked the mathematics that Euclid introduced in his Optics. Efforts by the Greeks prior to Euclid were concerned primarily with the physical dimension of vision. Whereas Plato and Empedocles thought of the visual ray as "luminous and ethereal emanation", Euclid’s treatment of vision in a mathematical way was part of the larger Hellenistic trend to quantify a whole range of scientific fields.
Because Optics contributed a new dimension to the study of vision, it influenced later scientists. In particular, Ptolemy used Euclid's mathematical treatment of vision and his idea of a visual cone in combination with physical theories in Ptolemy's Optics, which has been called "one of the most important works on optics written before Newton". Renaissance artists such as Brunelleschi, Alberti, and Dürer used Euclid's Optics in their own work on linear perspective.
Structure and method
Similar to Euclid's much more famous work on geometry, Elements, Optics begins with a small number of definitions and postulates, which are then used to prove, by deductive reasoning, a body of geometric propositions (theorems in modern terminology) about vision.
The postulates in Optics are:
Let it be assumed
1. That rectilinear rays proceeding from the eye diverge indefinitely;
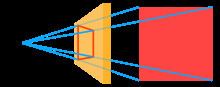
2. That the figure contained by a set of visual rays is a cone of which the vertex is at the eye and the base at the surface of the objects seen;
3. That those things are seen upon which visuals rays fall and those things are not seen upon which visual rays do not fall;
4. That things seen under a larger angle appear larger, those under a smaller angle appear smaller, and those under equal angles appear equal;
5. That things seen by higher visual rays appear higher, and things seen by lower visual rays appear lower;
6. That, similarly, things seen by rays further to the right appear further to the right, and things seen by rays further to the left appear further to the left;
The geometric treatment of the subject follows the same methodology as the Elements.
Content
According to Euclid, the eye sees objects that are within its visual cone. The visual cone is made up of straight lines, or visual rays, extending outward from the eye. These visual rays are discrete, but we perceive a continuous image because our eyes, and thus our visual rays, move very quickly. Because visual rays are discrete, however, it is possible for small objects to lie unseen between them. This accounts for the difficulty in searching for a dropped needle. Although the needle may be within one's field of view, until the eye's visual rays fall upon the needle, it will not be seen. Discrete visual rays also explain the sharp or blurred appearance of objects. According to postulate 7, the closer an object, the more visual rays fall upon it and the more detailed or sharp it appears. This is an early attempt to describe the phenomenon of optical resolution.
Much of the work considers perspective, how an object appears in space relative to the eye. For example, in proposition 8, Euclid argues that the perceived size of an object is not related to its distance from the eye by a simple proportion.
