 | ||
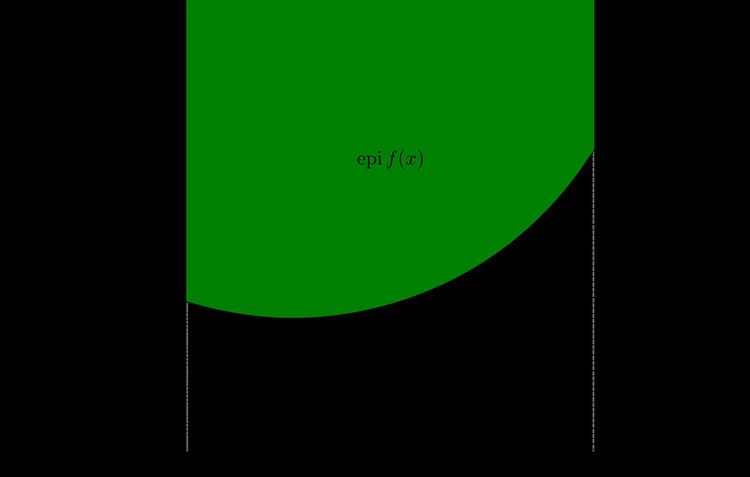
In mathematics, the epigraph or supergraph of a function f : Rn→R is the set of points lying on or above its graph:
The strict epigraph is the epigraph with the graph itself removed:
The same definitions are valid for a function that takes values in R ∪ ∞. In this case, the epigraph is empty if and only if f is identically equal to infinity.
The domain (rather than the co-domain) of the function is not particularly important for this definition; it can be any linear space or even an arbitrary set instead of
Similarly, the set of points on or below the function is its hypograph.
The epigraph can often be used to give geometrical intrepretations of the properties of convex functions or to prove these properties.
Properties
A function is convex if and only if its epigraph is a convex set. The epigraph of a real affine function g : Rn→R is a halfspace in Rn+1.
A function is lower semicontinuous if and only if its epigraph is closed.
