 | ||
Duncan's paradox is a thermodynamic thought experiment proposed by T. Duncan in 2000 that has connections to the second law of thermodynamics and catalysis. It was raised in response to an earlier theoretical proposal suggesting that certain gas-surface reactions (heterogeneous catalysis) can generate steady-state pressure gradients under low-pressure, sealed blackbody conditions. Duncan's paradox was devised to demonstrate the incompatibility of these purported pressure gradients with the second law of thermodynamics. Specifically, such pressure gradients would allow construction of perpetual motion machines of the second type; therefore, because such devices are presumed thermodynamically impossible, the enabling pressure gradients must also be impossible.
Contents
Pressure and Temperature Paradoxes
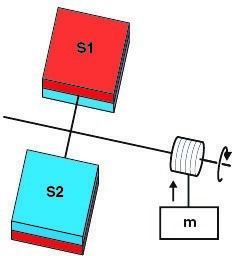
Duncan's paradox can be envisioned either in terms of pressure or temperature differences. Consider a dimeric gas (A2) that is susceptible to endothermic dissociation or exothermic recombination (A2 ↔ 2A). The gas is housed between two surfaces (S1 and S2), whose chemical reactivities are distinct with respect to the gas. Specifically, let S1 preferentially dissociate dimer A2 and desorb monomer A, while S2 preferentially recombines monomers A and desorbs dimer A2.
For the pressure paradox, let S1 and S2 cover the apposing faces of a radiometer, which is housed inside a sealed blackbody cavity, itself lined with S2 (Fig. 1). Let the surface area of the vanes be much less than that of the cavity walls so that the cavity gas concentrations are effectively set by the gas-surface reactions on the walls. Because S1 preferentially desorbs monomers compared with S2, and because two monomers are desorbed for every dimer, it can be shown, for a broad range of parameters, that there will be a greater gas pressure over the S1 than over the S2 vane faces. This steady-state pressure differential turns the radiometer and can be harnessed to perform steady-state work; in this case (Fig. 1), a weight is lifted against gravity. Appealing to the first law of thermodynamics, it can be shown that this steady-state work must come ultimately from heat from the heat bath; however, this contradicts the Kelvin-Planck form of the second law, which forbids the conversion of heat solely into work in a thermodynamic cycle such as this. Thus, if the second law is inviolable, such pressure differences must be thermodynamically impossible.
Duncan's temperature paradox follows similarly from this. Here, surface desorbed A2 and A set up a convective cycle between S1 and S2 (Fig. 2). S1 provides an excess of A to S2, while S2 provides an excess of A2 to S1. Because the reaction A2 → 2A is endothermic—and its reverse exothermic—it follows that S1 cools down and S2 heats up. The permanent temperature difference thus established between S1 and S2 can be harnessed via a heat engine (e.g., a thermoelectric device) to perform work, again as before, at the ultimate expense of the surrounding heat bath and in violation of the Kelvin-Planck form of the second law. As proposed by Duncan for his pressure paradox, this temperature paradox also would be resolved by forbidding the existence of differential gas-surface products between different surface types.
Laboratory Tests and Theoretical Support
In 2014 Duncan's temperature paradox was experimentally realized, utilizing hydrogen dissociation on high-temperature transition metals (tungsten and rhenium). Ironically, these experiments support the predictions of the paradox and provide laboratory evidence for second law breakdown. These results are corroborated by other experiments that demonstrate anomalous (and differential) levels of hydrogen dissociation on heated transition metals; additional theoretical support can be found in the theory of epicatalysis.
In 2015 Laboratory experiments verified examples of room temperature epicatalysis involving hydrogen-bonded diamonds on polymers. This could open the door to room temperature tests of Duncan's Paradox
