 | ||
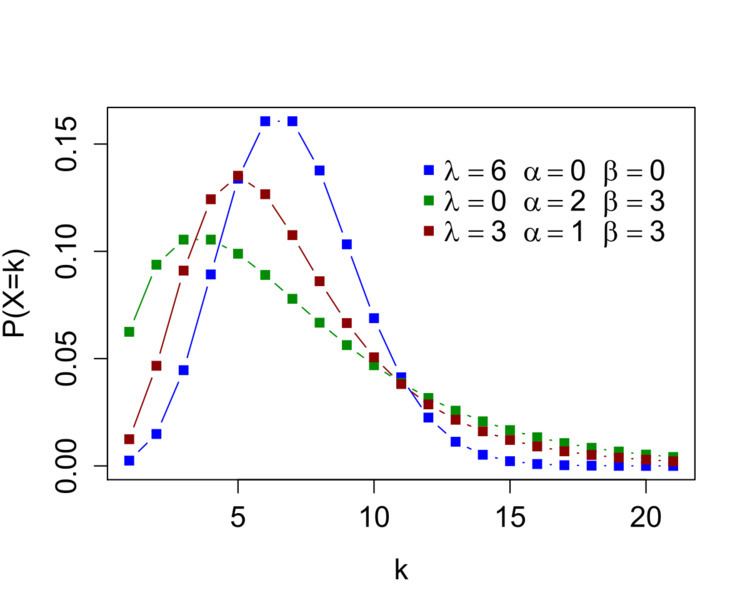
Parameters λ > 0 {\displaystyle \lambda >0} (fixed mean) α , β > 0 {\displaystyle \alpha ,\beta >0} (parameters of variable mean) Support k ∈ { 0 , 1 , 2 , … } {\displaystyle k\in \{0,1,2,\ldots \}} pmf ∑ i = 0 k Γ ( α + i ) β i λ k − i e − λ Γ ( α ) i ! ( 1 + β ) α + i ( k − i ) ! {\displaystyle \sum _{i=0}^{k}{\frac {\Gamma (\alpha +i)\beta ^{i}\lambda ^{k-i}e^{-\lambda }}{\Gamma (\alpha )i!(1+\beta )^{\alpha +i}(k-i)!}}} CDF ∑ j = 0 k ∑ i = 0 j Γ ( α + i ) β i λ j − i e − λ Γ ( α ) i ! ( 1 + β ) α + i ( j − i ) ! {\displaystyle \sum _{j=0}^{k}\sum _{i=0}^{j}{\frac {\Gamma (\alpha +i)\beta ^{i}\lambda ^{j-i}e^{-\lambda }}{\Gamma (\alpha )i!(1+\beta )^{\alpha +i}(j-i)!}}} Mean λ + α β {\displaystyle \lambda +\alpha \beta } Mode { z , z + 1 { z ∈ Z } : z = ( α − 1 ) β + λ ⌊ z ⌋ otherwise {\displaystyle {\begin{cases}z,z+1&\{z\in \mathbb {Z} \}:\;z=(\alpha -1)\beta +\lambda \\\lfloor z\rfloor &{\textrm {otherwise}}\end{cases}}} | ||
The Delaporte distribution is a discrete probability distribution that has received attention in actuarial science. It can be defined using the convolution of a negative binomial distribution with a Poisson distribution. Just as the negative binomial distribution can be viewed as a Poisson distribution where the mean parameter is itself a random variable with a gamma distribution, the Delaporte distribution can be viewed as a compound distribution based on a Poisson distribution, where there are two components to the mean parameter: a fixed component, which has the
Properties
The skewness of the Delaporte distribution is:
The excess kurtosis of the distribution is:
