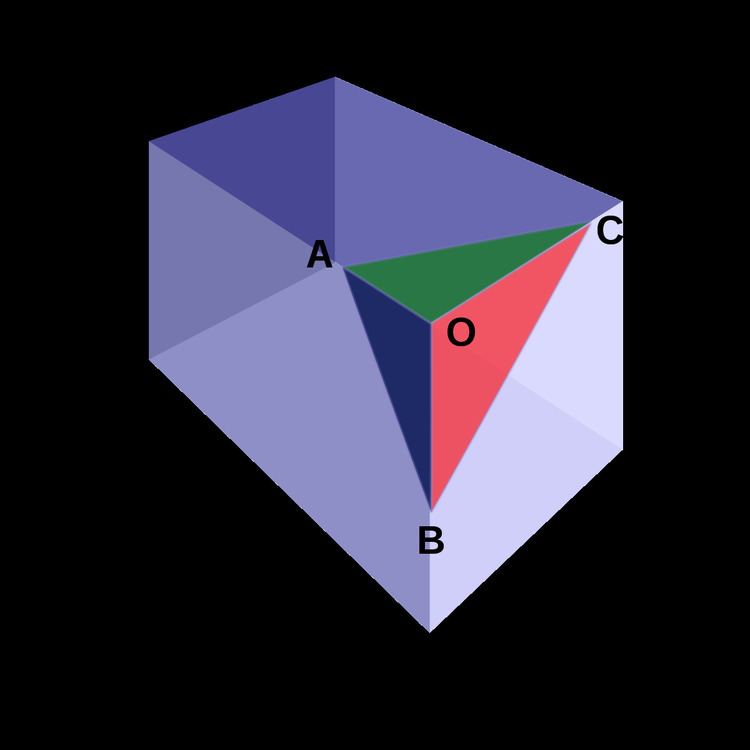
 | ||
De Gua's theorem is a three-dimensional analog of the Pythagorean theorem and named for Jean Paul de Gua de Malves.
Contents
If a tetrahedron has a right-angle corner (like the corner of a cube), then the square of the area of the face opposite the right-angle corner is the sum of the squares of the areas of the other three faces.
Generalizations
The Pythagorean theorem and de Gua's theorem are special cases (n = 2, 3) of a general theorem about n-simplices with a right-angle corner. This, in turn, is a special case of a yet more general theorem by Donald R. Conant and William A. Beyer, which can be stated as follows.
Let U be a measurable subset of a k-dimensional affine subspace of
where
De Gua's theorem and its generalisation (above) to n-simplices with right-angle corners correspond to the special case where k = n−1 and U is an (n−1)-simplex in
which is de Gua's theorem.
History
Jean Paul de Gua de Malves (1713–85) published the theorem in 1783, but around the same time a slightly more general version was published by another French mathematician, Charles de Tinseau d'Amondans (1746–1818), as well. However the theorem had also been known much earlier to Johann Faulhaber (1580–1635) and René Descartes (1596–1650).
