 | ||
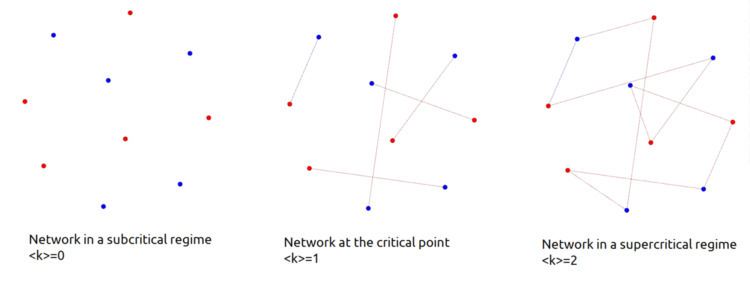
In network science, a critical point is a value of average degree, which separates random networks that have a giant component from those that do not (i.e. it separates a network in a subcritical regime from one in a supercritical regime). Considering a random network with an average degree
Contents
where the average degree is defined by the fraction of the number of edges (
Subcritical regime
In a subcritical regime the network has no giant component, only small clusters. In the special case of
Supercritical regime
In a supercritical regime, in contrary to the subcritical regime the network has a giant component. In the special case of
Example on different regimes
Consider a speed dating event as an example, with the participants as the nodes of the network. At the beginning of the event, people do not know anyone else. In this case the network is in a subcritical regime, that is, there is no giant component in the network (even if there are a couple of people, who know each other). After the first round of dates, everyone knows exactly one other person. There is still no giant component in the network, the average degree is
