 | ||
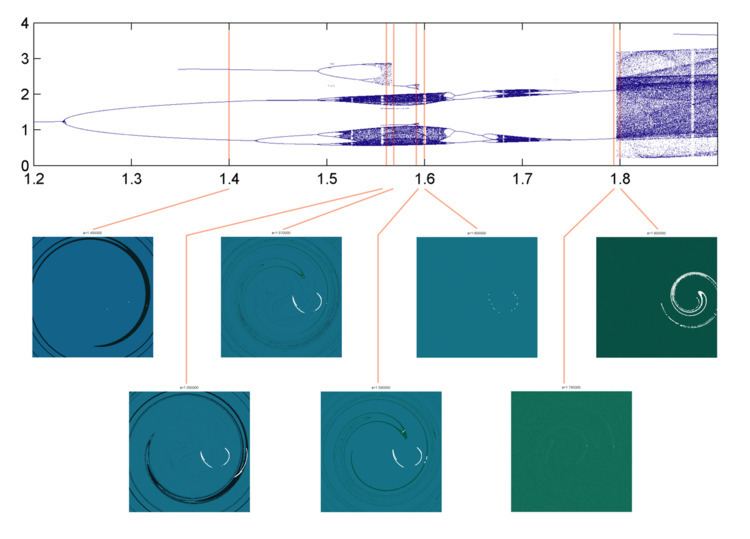
In applied mathematics and Astrodynamics, in the theory of dynamical systems, a crisis is the sudden appearance or disappearance of a strange attractor as the parameters of a dynamical system are varied. This global bifurcation occurs when a chaotic attractor comes into contact with an unstable periodic orbit or its stable manifold. As the orbit approaches the unstable orbit it will diverge away from the previous attractor, leading to a qualitatively different behaviour. Crises can produce intermittent behaviour.
Grebogi, Ott, Romeiras, and Yorke distinguished between three types of crises:
Note that the reverse case (sudden appearance, shrinking or splitting of attractors) can also occur. The latter two crises are sometimes called explosive bifurcations.
While crises are "sudden" as a parameter is varied, the dynamics of the system over time can show long transients before orbits leave the neighbourhood of the old attractor. Typically there is a time constant τ for the length of the transient that diverges as a power law (τ ≈ |p − pc|γ) near the critical parameter value pc. The exponent γ is called the critical crisis exponent. There also exist systems where the divergence is stronger than a power law, so-called super-persistent chaotic transients.
